题目内容
6. 如图,正方形ABCD中,点M为DA延长线上一点,连接BM,过点C作CN∥BM,交AD于点N,在CD延长线上取一点F,使BM=CF-DN,连接BF,交CN于点E.
如图,正方形ABCD中,点M为DA延长线上一点,连接BM,过点C作CN∥BM,交AD于点N,在CD延长线上取一点F,使BM=CF-DN,连接BF,交CN于点E.求证:BC=EC.
分析 过点B作BG⊥CN,交CD于点G,先证明△BCG≌△CDN,得出BG=CN,CG=DN,再证出CN=BM,得出BG=FG,得出∠FBG=∠F 然后证出∠EBC=∠BEC,即可得出结论.
解答 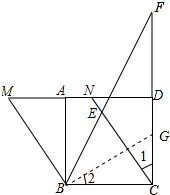 证明:过点B作BG⊥CN,交CD于点G,则∠2+∠BCN=90°,
证明:过点B作BG⊥CN,交CD于点G,则∠2+∠BCN=90°,
∵四边形ABCD是正方形,
∴BC=CD,∠BCD=∠CDA=90°,
即∠1+∠BCN=90°,
∴∠2=∠1,
在△BCG和△CDN中,$\left\{\begin{array}{l}{∠2=∠1}&{\;}\\{BC=CD}&{\;}\\{∠BCG=∠CDN}&{\;}\end{array}\right.$,
∴△BCG≌△CDN(ASA),
∴BG=CN,CG=DN,
∵MN∥BC,BM∥CN,
∴四边形BCNM是平行四边形,
∴CN=BM,
∴BG=BM=CF-DN=CF-CG=FG,
∴∠FBG=∠F,
∵∠EBC=∠2+∠FBG,∠BEC=∠1+∠F,
∴∠EBC=∠BEC,
∴BC=EC.
点评 本题考查了正方形的性质、全等三角形的判定及性质、平行四边形的判定及性质、等腰三角形的判定;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
9.计算(a2b)3的结果是( )
| A. | a6b3 | B. | a2b3 | C. | a5b3 | D. | a6b |
10.在平面直角坐标系中,点P(-3,2)关于直线y=x对称点的坐标是( )
| A. | (-3,-2) | B. | (3,2) | C. | (2,-3) | D. | (3,-2) |
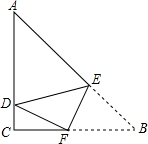 如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=8,E、F分别为AB、AC上的点,沿直线EF将∠B折叠,使点B恰好落在AC上的D处,当△ADE恰好为直角三角形时,BE的长为$\frac{15}{4}$或$\frac{30}{7}$.
如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=8,E、F分别为AB、AC上的点,沿直线EF将∠B折叠,使点B恰好落在AC上的D处,当△ADE恰好为直角三角形时,BE的长为$\frac{15}{4}$或$\frac{30}{7}$.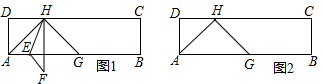
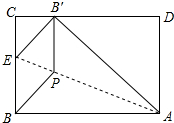 将矩形纸片ABCD折叠,使点B落在边CD上的B′处,折痕为AE,过B′作B′P∥BC,交AE于点P,连接BP.已知BC=3,CB′=1,下列结论:
将矩形纸片ABCD折叠,使点B落在边CD上的B′处,折痕为AE,过B′作B′P∥BC,交AE于点P,连接BP.已知BC=3,CB′=1,下列结论: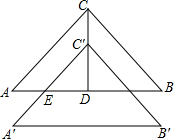 如图,Rt△ABC中,∠ACB=90°,CA=CB,AB=8,D是线段AB上的一个动点,将Rt△ABC由点C到点D的方向平移2个单位得到Rt△A′B′C′,且C′A′与AB交于点E.
如图,Rt△ABC中,∠ACB=90°,CA=CB,AB=8,D是线段AB上的一个动点,将Rt△ABC由点C到点D的方向平移2个单位得到Rt△A′B′C′,且C′A′与AB交于点E. 已知,如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,连接DE.
已知,如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,连接DE.