题目内容
7.已知△ABC内接于⊙O,∠A=45°,BC=2,求⊙O的半径.分析 根据题意画出图形,连接OB,OC,根据圆周角定理求出∠BOC的度数,再根据勾股定理即可得出结论.
解答  解:如图所示,连接OB,OC,
解:如图所示,连接OB,OC,
∵∠A=45°,BC=2,
∴∠BOC=90°,
∵OB=OC,
∴2OB2=BC2,即2OB2=22,解得OB=1,即⊙O的半径为1.
点评 本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
13.若a=$\frac{1}{\sqrt{2}}$,b=$\frac{\sqrt{2}}{2}$,则( )
| A. | a=b | B. | a、b互为倒数 | C. | ab=2 | D. | a、b互为相反数 |
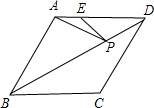 如图,在菱形ABCD中,AB=6,∠ABC=60°,点E在AD上,且AE=2,点P是对角线BD上的一个动点,则PE+PA的最小值是2$\sqrt{7}$.
如图,在菱形ABCD中,AB=6,∠ABC=60°,点E在AD上,且AE=2,点P是对角线BD上的一个动点,则PE+PA的最小值是2$\sqrt{7}$.