题目内容
14.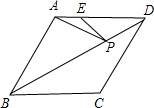 如图,在菱形ABCD中,AB=6,∠ABC=60°,点E在AD上,且AE=2,点P是对角线BD上的一个动点,则PE+PA的最小值是2$\sqrt{7}$.
如图,在菱形ABCD中,AB=6,∠ABC=60°,点E在AD上,且AE=2,点P是对角线BD上的一个动点,则PE+PA的最小值是2$\sqrt{7}$.
分析 连接AC、CE,交BD于P,根据菱形的性质,A、C关于直线BD对称,得出PA=PC,则PA+PE=PC+PE=CE,根据两点之间线段最短,则CE就是PE+PA的最小值,作CF⊥AD于F,求得CF、EF的长,根据勾股定理即可求得.
解答  解:连接AC、CE,交BD于P,
解:连接AC、CE,交BD于P,
∵四边形ABCD是菱形,
∴A、C关于直线BD对称,
∴PA=PC,
∴PA+PE=PC+PE=CE,
根据两点之间线段最短,则CE就是PE+PA的最小值,
作CF⊥AD于F,
∵在菱形ABCD中,AB=6,∠ABC=60°,
∴△ACD是等边三角形,CF=sin60°•AC=$\frac{\sqrt{3}}{2}$×6=3$\sqrt{3}$,
∴AF=DF=$\frac{1}{2}$AD=3,CF=sin60°•AC=$\frac{\sqrt{3}}{2}$×6=3$\sqrt{3}$,
∵AE=2,
∴EF=1,
在RT△ECF中,CE=$\sqrt{E{F}^{2}+C{E}^{2}}$=$\sqrt{{1}^{2}+(3\sqrt{3})^{2}}$=2$\sqrt{7}$.
∴PE+PA的最小值为2$\sqrt{7}$.
点评 本题考查的是轴对称-最短路线问题,等边三角形的性质,解直角三角形以及勾股定理等,熟知“两点之间线段最短”是解答此题的关键.

练习册系列答案
相关题目
3.已知点M(-2,4)在双曲线y=$\frac{m+4}{x}$上,则下列各点一定在该双曲线上的是( )
| A. | (-2,-4) | B. | (4,-2) | C. | (2,4) | D. | (4,2) |
 已知:如图,AB∥CD,AC与BD相交于E,若CE=2,AE=3,AB=5,BD=$\frac{20}{3}$,求sinA的值.
已知:如图,AB∥CD,AC与BD相交于E,若CE=2,AE=3,AB=5,BD=$\frac{20}{3}$,求sinA的值. (1)如图所示,在平面直角坐标系中,描出下列3个点,A(-1,0),B(5,0),C(3,4);
(1)如图所示,在平面直角坐标系中,描出下列3个点,A(-1,0),B(5,0),C(3,4);
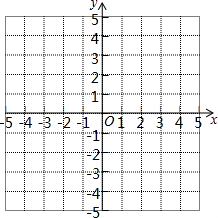 在如图的直角坐标系中,画出点A(-1,-1),B(3,-1),C(4,2),D(0,2),并将各点依次用线段连接起来,求图形ABCD的面积.(每个小方格的长和宽都为一个长度单位)
在如图的直角坐标系中,画出点A(-1,-1),B(3,-1),C(4,2),D(0,2),并将各点依次用线段连接起来,求图形ABCD的面积.(每个小方格的长和宽都为一个长度单位)