题目内容
19.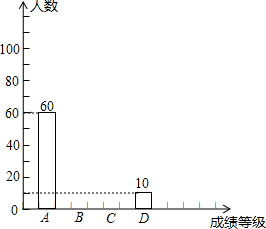 为了迎接党的十八大的召开,某校组织了以“党在我心中”为主题的征文比赛,每位学生只能参加一次比赛,比赛成绩分A、B、C、D四个等级.随机抽取该校部分学生的征文比赛成绩进行统计分析,并绘制了如下的统计图表:
为了迎接党的十八大的召开,某校组织了以“党在我心中”为主题的征文比赛,每位学生只能参加一次比赛,比赛成绩分A、B、C、D四个等级.随机抽取该校部分学生的征文比赛成绩进行统计分析,并绘制了如下的统计图表:| 成绩等级 | A | B | C | D |
| 人数 | 60 | x | y | 10 |
| 占抽查学生总数的百分比 | 30% | 50% | 15% | m |
(1)本次抽查的学生共有200名;
(2)表中x、y和m所表示的数分别为:X=100,y=30,m=5%;补全条形统计图;
(3)若获得A、B、C、D四个等级按分值分别记为每人5分、4分、3分、2分,现选取A等2人,B等2人,C等1人,D等1人组成6人小团队,利用树形图或列表法,求在这6人中随机抽取2人,2人分数之和不低于8分的概率.
分析 (1)用A组的人数除以该组所占的百分比即可求得抽查的总人数;
(2)用总人数乘以B、C两组所占的百分比即可求得x、y的值,用整体1减去A、B、C等级人数所占的百分比,即可求出m;
(3)根据题意先列出图表,再根据概率公式进行计算即可.
解答 解:(1)根据图表可知:A组有60人,占总数的30%,
则抽查的总人数为:60÷30%=200人;
故答案为:200;
(2)根据题意得:
x=200×50%=100人,
y=200×15%=30人,
m=10÷200×100%=5%;
故答案为:100,30,5%;
(3)根据题意得:2人分数之和的结果列表如下:
| A | A | B | B | C | D | |
| A | 10 | 9 | 9 | 8 | 7 | |
| A | 10 | 9 | 9 | 8 | 7 | |
| B | 9 | 9 | 8 | 7 | 6 | |
| B | 9 | 9 | 8 | 7 | 6 | |
| C | 8 | 8 | 7 | 7 | 5 | |
| D | 7 | 7 | 6 | 6 | 5 |
则2人分数之和不低于8分的概率是$\frac{16}{30}$=$\frac{8}{15}$.
点评 本题考查了条形统计图的知识,仔细的观察统计图并从统计图中整理出进一步解题的有关信息是本题的关键.

练习册系列答案
相关题目
7.下表,填在各正方形中的四个数之间都有相同的规律,根据此规律,m的值是( )


| A. | 66 | B. | 112 | C. | 58 | D. | 74 |
 如图,AB是⊙O的直径,弦CD⊥AB,∠AOD=60°,CD=4$\sqrt{3}$cm.则图中阴影部分的面积S阴影=$\frac{8}{3}$.
如图,AB是⊙O的直径,弦CD⊥AB,∠AOD=60°,CD=4$\sqrt{3}$cm.则图中阴影部分的面积S阴影=$\frac{8}{3}$. 如图,已知在圆心角为120的扇形AOB中,点C,D,E都在扇形AOB的弧上,且AC=DE=2$\sqrt{3}$,CD=EB=2,则这个扇形的面积为$\frac{28}{3}$π.
如图,已知在圆心角为120的扇形AOB中,点C,D,E都在扇形AOB的弧上,且AC=DE=2$\sqrt{3}$,CD=EB=2,则这个扇形的面积为$\frac{28}{3}$π.