题目内容
11. 如图,已知在圆心角为120的扇形AOB中,点C,D,E都在扇形AOB的弧上,且AC=DE=2$\sqrt{3}$,CD=EB=2,则这个扇形的面积为$\frac{28}{3}$π.
如图,已知在圆心角为120的扇形AOB中,点C,D,E都在扇形AOB的弧上,且AC=DE=2$\sqrt{3}$,CD=EB=2,则这个扇形的面积为$\frac{28}{3}$π.
分析 连接AD,作DF垂直于AC的延长线于F,先证得△AOD是等边三角形,得出AD等于半径,解直角三角形求得DF=1,CF=$\sqrt{3}$,然后根据勾股定理即可求得AD(半径),然后根据扇形的面积公式即可求得.
解答  解:连接AD,作DF垂直于AC的延长线于F,
解:连接AD,作DF垂直于AC的延长线于F,
∵圆心角为120的扇形AOB中,AC=DE=2$\sqrt{3}$,CD=EB=2,
∴∠AOD=60°,
∴∠ACD=150°,
∴∠FCD=30°,
∵OA=OD,
∴△AOD是等边三角形,
∴AD=OA=OD,
∵∠AFD=90°,CD=2,∠FCD=30°,
∴DF=$\frac{1}{2}$CD=1,CF=$\frac{\sqrt{3}}{2}$CD=$\sqrt{3}$,
∴AF=AC+CF=2$\sqrt{3}$+$\sqrt{3}$=3$\sqrt{3}$,
∴AD=$\sqrt{A{F}^{2}+D{F}^{2}}$=$\sqrt{(3\sqrt{3})^{2}+{1}^{2}}$=2$\sqrt{7}$,
∴扇形的半径为2$\sqrt{7}$,
∴S=$\frac{120π×(2\sqrt{7)^{2}}}{360}$=$\frac{28}{3}$π.
点评 本题考查了等边三角形的判定和性质,特殊角的三角函数,勾股定理的应用研究扇形的面积等,作出辅助线构建直角三角形是解题的关键.

练习册系列答案
相关题目
19.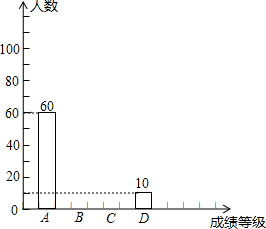 为了迎接党的十八大的召开,某校组织了以“党在我心中”为主题的征文比赛,每位学生只能参加一次比赛,比赛成绩分A、B、C、D四个等级.随机抽取该校部分学生的征文比赛成绩进行统计分析,并绘制了如下的统计图表:
为了迎接党的十八大的召开,某校组织了以“党在我心中”为主题的征文比赛,每位学生只能参加一次比赛,比赛成绩分A、B、C、D四个等级.随机抽取该校部分学生的征文比赛成绩进行统计分析,并绘制了如下的统计图表:
根据表中的信息,解决下列问题:
(1)本次抽查的学生共有200名;
(2)表中x、y和m所表示的数分别为:X=100,y=30,m=5%;补全条形统计图;
(3)若获得A、B、C、D四个等级按分值分别记为每人5分、4分、3分、2分,现选取A等2人,B等2人,C等1人,D等1人组成6人小团队,利用树形图或列表法,求在这6人中随机抽取2人,2人分数之和不低于8分的概率.
 为了迎接党的十八大的召开,某校组织了以“党在我心中”为主题的征文比赛,每位学生只能参加一次比赛,比赛成绩分A、B、C、D四个等级.随机抽取该校部分学生的征文比赛成绩进行统计分析,并绘制了如下的统计图表:
为了迎接党的十八大的召开,某校组织了以“党在我心中”为主题的征文比赛,每位学生只能参加一次比赛,比赛成绩分A、B、C、D四个等级.随机抽取该校部分学生的征文比赛成绩进行统计分析,并绘制了如下的统计图表:| 成绩等级 | A | B | C | D |
| 人数 | 60 | x | y | 10 |
| 占抽查学生总数的百分比 | 30% | 50% | 15% | m |
(1)本次抽查的学生共有200名;
(2)表中x、y和m所表示的数分别为:X=100,y=30,m=5%;补全条形统计图;
(3)若获得A、B、C、D四个等级按分值分别记为每人5分、4分、3分、2分,现选取A等2人,B等2人,C等1人,D等1人组成6人小团队,利用树形图或列表法,求在这6人中随机抽取2人,2人分数之和不低于8分的概率.
3.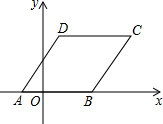 如图坐标系,四边形ABCD是菱形,顶点A、B在x轴上,AB=5,点C在第一象限,且菱形ABCD的面积为20,A坐标为(-2,0),则顶点C的坐标为( )
如图坐标系,四边形ABCD是菱形,顶点A、B在x轴上,AB=5,点C在第一象限,且菱形ABCD的面积为20,A坐标为(-2,0),则顶点C的坐标为( )
 如图坐标系,四边形ABCD是菱形,顶点A、B在x轴上,AB=5,点C在第一象限,且菱形ABCD的面积为20,A坐标为(-2,0),则顶点C的坐标为( )
如图坐标系,四边形ABCD是菱形,顶点A、B在x轴上,AB=5,点C在第一象限,且菱形ABCD的面积为20,A坐标为(-2,0),则顶点C的坐标为( )| A. | (4,3) | B. | (5,4) | C. | (6,4) | D. | (7,3) |
 如图,平行四边形ABCD中,AB=5,AD=3,AE平分∠DAB交BC的延长线于F点,求CF的长.
如图,平行四边形ABCD中,AB=5,AD=3,AE平分∠DAB交BC的延长线于F点,求CF的长.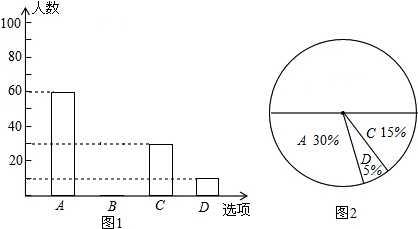
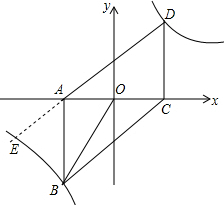 如图,在平面直角坐标系中,点 A、C关于原点O对称,分别过点A、C作x轴的垂线,它们与反比例函数y=$\frac{k}{x}$的图象交于点B、D,连结AD、BC,若C点的坐标为(m,0)
如图,在平面直角坐标系中,点 A、C关于原点O对称,分别过点A、C作x轴的垂线,它们与反比例函数y=$\frac{k}{x}$的图象交于点B、D,连结AD、BC,若C点的坐标为(m,0)