题目内容
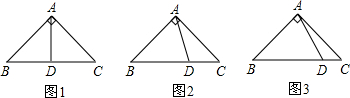
8.已知,如图,Rt△ABC,∠BAC=90°,AB=AC,BC=6,D为直线BC上一点(1)如图1,若BD=CD,则AD=3;
(2)如图2,若BD=2CD,求AD的值;
(3)如图3,若BD=mCD,请直接写出AD的值为$\frac{3\sqrt{{m}^{2}+2m+5}}{m+1}$(用含m的式子表示)
分析 (1)根据三线合一定理即可求解;
(2)作AE⊥BC,求得AE和DC即可求得ED的长,在直角△AED中利用勾股定理求解;
(3)与(2)的解法相同.
解答 解:(1)∵Rt△ABC,∠BAC=90°,AB=AC,BD=CD,
∴AD=$\frac{1}{2}$BC=$\frac{1}{2}$×6=3.
故答案是:3;
(2) 作AE⊥BC,则AE=$\frac{1}{2}$BC=3,
作AE⊥BC,则AE=$\frac{1}{2}$BC=3,
∵BD=2CD,
∴CD=$\frac{1}{3}$BC=$\frac{1}{3}$×3=1,
∴ED=1,
∴在直角△AED中,AD=$\sqrt{A{E}^{2}+E{D}^{2}}$=$\sqrt{10}$;
(3)同理,作AF⊥BC,则AF=3,
∵BD=mCD,
∴DC=$\frac{1}{1+m}$BC=$\frac{6}{1+m}$,
∴在直角△ADF中,AD=$\sqrt{A{F}^{2}+D{F}^{2}}$=$\sqrt{{3}^{2}+(\frac{6}{1+m})^{2}}$=$\frac{3\sqrt{{m}^{2}+2m+5}}{m+1}$.
故答案是:$\frac{3\sqrt{{m}^{2}+2m+5}}{m+1}$.
点评 本题考查了等腰三角形的性质:三线合一定理,以及勾股定理,求线段长的问题常用的方法是转化为解直角三角形的问题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
19. 为了迎接党的十八大的召开,某校组织了以“党在我心中”为主题的征文比赛,每位学生只能参加一次比赛,比赛成绩分A、B、C、D四个等级.随机抽取该校部分学生的征文比赛成绩进行统计分析,并绘制了如下的统计图表:
为了迎接党的十八大的召开,某校组织了以“党在我心中”为主题的征文比赛,每位学生只能参加一次比赛,比赛成绩分A、B、C、D四个等级.随机抽取该校部分学生的征文比赛成绩进行统计分析,并绘制了如下的统计图表:
根据表中的信息,解决下列问题:
(1)本次抽查的学生共有200名;
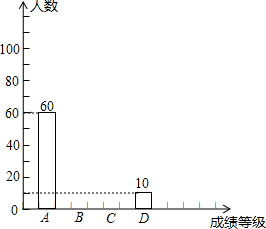
(2)表中x、y和m所表示的数分别为:X=100,y=30,m=5%;补全条形统计图;
(3)若获得A、B、C、D四个等级按分值分别记为每人5分、4分、3分、2分,现选取A等2人,B等2人,C等1人,D等1人组成6人小团队,利用树形图或列表法,求在这6人中随机抽取2人,2人分数之和不低于8分的概率.
 为了迎接党的十八大的召开,某校组织了以“党在我心中”为主题的征文比赛,每位学生只能参加一次比赛,比赛成绩分A、B、C、D四个等级.随机抽取该校部分学生的征文比赛成绩进行统计分析,并绘制了如下的统计图表:
为了迎接党的十八大的召开,某校组织了以“党在我心中”为主题的征文比赛,每位学生只能参加一次比赛,比赛成绩分A、B、C、D四个等级.随机抽取该校部分学生的征文比赛成绩进行统计分析,并绘制了如下的统计图表:| 成绩等级 | A | B | C | D |
| 人数 | 60 | x | y | 10 |
| 占抽查学生总数的百分比 | 30% | 50% | 15% | m |
(1)本次抽查的学生共有200名;
(2)表中x、y和m所表示的数分别为:X=100,y=30,m=5%;补全条形统计图;
(3)若获得A、B、C、D四个等级按分值分别记为每人5分、4分、3分、2分,现选取A等2人,B等2人,C等1人,D等1人组成6人小团队,利用树形图或列表法,求在这6人中随机抽取2人,2人分数之和不低于8分的概率.
3.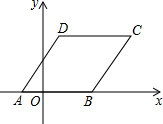 如图坐标系,四边形ABCD是菱形,顶点A、B在x轴上,AB=5,点C在第一象限,且菱形ABCD的面积为20,A坐标为(-2,0),则顶点C的坐标为( )
如图坐标系,四边形ABCD是菱形,顶点A、B在x轴上,AB=5,点C在第一象限,且菱形ABCD的面积为20,A坐标为(-2,0),则顶点C的坐标为( )
 如图坐标系,四边形ABCD是菱形,顶点A、B在x轴上,AB=5,点C在第一象限,且菱形ABCD的面积为20,A坐标为(-2,0),则顶点C的坐标为( )
如图坐标系,四边形ABCD是菱形,顶点A、B在x轴上,AB=5,点C在第一象限,且菱形ABCD的面积为20,A坐标为(-2,0),则顶点C的坐标为( )| A. | (4,3) | B. | (5,4) | C. | (6,4) | D. | (7,3) |
 如图,根据题意填空
如图,根据题意填空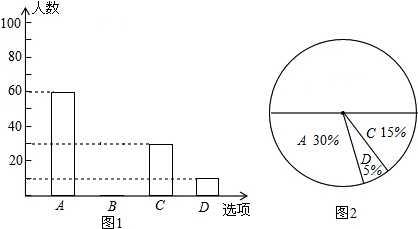
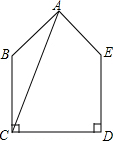 如图,面积为72的五边形ABCDE中,BC=DE=7,CD=8,∠BCD=∠EDC=90°,连接对角线AC,则AC+AE的最小值为17.
如图,面积为72的五边形ABCDE中,BC=DE=7,CD=8,∠BCD=∠EDC=90°,连接对角线AC,则AC+AE的最小值为17.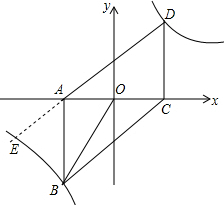 如图,在平面直角坐标系中,点 A、C关于原点O对称,分别过点A、C作x轴的垂线,它们与反比例函数y=$\frac{k}{x}$的图象交于点B、D,连结AD、BC,若C点的坐标为(m,0)
如图,在平面直角坐标系中,点 A、C关于原点O对称,分别过点A、C作x轴的垂线,它们与反比例函数y=$\frac{k}{x}$的图象交于点B、D,连结AD、BC,若C点的坐标为(m,0) 如图,内外两个四边形都是正方形,阴影部分的宽为4,且面积为56,则内部小正方的面积是?
如图,内外两个四边形都是正方形,阴影部分的宽为4,且面积为56,则内部小正方的面积是?