题目内容
19.直线y=2x+b与直线y=kx+5交于点(-2,-3),求:(1)两直线的表达式;
(2)画出两直线的图象;
(3)求这两条直线与x轴围成的三角形面积.
分析 (1)把点(-2,-3)分别代入直线y=2x+b与直线y=kx+5求得解析式即可;
(2)利用一次函数的性质画出图象即可;
(3)求得两条直线与x轴的交点坐标,进一步计算三角形面积即可.
解答 解:(1)把点(-2,-3)分别代入直线y=2x+b与直线y=kx+5,
得-3=2×(-2)+b,-3=-2k+5,
解得b=1,k=4,
所以直线y=2x+1,直线y=4x+5;
(2)图象如下: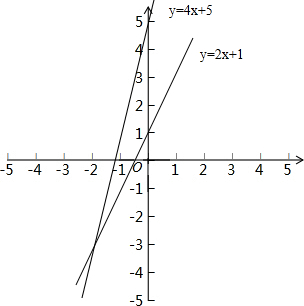
(3)直线y=2x+1与x轴交点坐标为(-$\frac{1}{2}$,0),直线y=4x+5与x轴交点坐标为(-$\frac{5}{4}$,0);
这两条直线与x轴围成的三角形面积=$\frac{1}{2}$×3×($\frac{5}{4}$-$\frac{1}{2}$)=$\frac{9}{8}$.
点评 本题考查的是用待定系数法求一次函数的解析式,一次函数图象上点的坐标特征,比较简单.求三角形的面积时要先画出图形,利用数形结合解答.

练习册系列答案
相关题目
 △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示. 如图,在平面直角坐标系中,菱形OABC的顶点B在x轴上,其坐标为(6,0),菱形的面积为18$\sqrt{3}$
如图,在平面直角坐标系中,菱形OABC的顶点B在x轴上,其坐标为(6,0),菱形的面积为18$\sqrt{3}$