题目内容
8. 如图,在平面直角坐标系中,菱形OABC的顶点B在x轴上,其坐标为(6,0),菱形的面积为18$\sqrt{3}$
如图,在平面直角坐标系中,菱形OABC的顶点B在x轴上,其坐标为(6,0),菱形的面积为18$\sqrt{3}$(1)写出A、C两点坐标并求出过B、C两点的直线l的函数关系式;
(2)求过O、A、B三点的抛物线的解析式;
(3)P为(1)中l上动点.横坐标为m、Q、R均在l的左侧,△PQR与△AOB全等且PQ∥x轴,求△PQR与菱形OABC重叠部分的面积S与m的函数关系式;
(4)直接写出△PQR与(2)中的抛物线有两个公共点时m的取值.
分析 (1)如图1中,连接AC交x轴于K.根据菱形的面积公式,求出AC的长,即可求出A、C两点坐标,利用待定系数法即可求出直线BC的解析式.
(2)可以假设抛物线的解析式为y=a(x-3)2+3$\sqrt{3}$,把(0,0)代入求出a即可.
(3)分两种情形①当3<m<6时,重叠部分是四边形PMOR,②如图3中,当6≤m<9时,重叠部分是△AQM.分别求解即可.
(4)如图4中,只要求出图中M、N两点坐标即可根据图象解决问题.
解答 解:(1)如图1中,连接AC交x轴于K.
∵四边形ABCD是菱形,面积为18$\sqrt{3}$,OB=6,
∴AC⊥OB,AK=KC,OK=KB,
∴$\frac{1}{2}$•OB•AC=18$\sqrt{3}$,
∴AC=6$\sqrt{3}$,
∴AK=3$\sqrt{3}$,
∴tan∠BAK=$\frac{BK}{AK}$=$\frac{\sqrt{3}}{3}$,
∴∠BAK=∠OAK=30°,
∴∠OAB=60°,
∴△OAB,△OBC是等边三角形,
∴A(3,3$\sqrt{3}$),C(3,-3$\sqrt{3}$),
设直线BC的解析式为y=kx+b,则有$\left\{\begin{array}{l}{3k+b=-3\sqrt{3}}\\{6k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\sqrt{3}}\\{b=-6\sqrt{3}}\end{array}\right.$,
∴直线BC的解析式为y=$\sqrt{3}$x-6$\sqrt{3}$.
(2)∵抛物线的顶点为(3,3$\sqrt{3}$),
∴可以假设抛物线的解析式为y=a(x-3)2+3$\sqrt{3}$,把(0,0)代入得到a=-$\frac{\sqrt{3}}{3}$,
∴y=-$\frac{\sqrt{3}}{3}$(x-3)2+3$\sqrt{3}$,
即y=-$\frac{\sqrt{3}}{3}$x2+2$\sqrt{3}$x.
(3)如图2中,∵△AOB是等边三角形,△PQR≌△BOA,PQ∥OB,
∴∠CPM=∠OBC=60°,∠ABC=∠RPC=120°,
∴AB∥PR,PQ∥BC,R、Q在直线OA上,
①当3<m<6时,重叠部分是四边形PMOR,
∴S=S△PQR-S△OMQ=9$\sqrt{3}$-$\frac{\sqrt{3}}{4}$(12-2m)2=-$\sqrt{3}$m2+12$\sqrt{3}$m-27$\sqrt{3}$.
②如图3中,当6≤m<9时,重叠部分是△AQM.
S=S△AQM=$\frac{\sqrt{3}}{4}$QM2=$\frac{\sqrt{3}}{4}$(18-2m)2=$\sqrt{3}$m2-18$\sqrt{3}$m+81$\sqrt{3}$.
综上所述,S=$\left\{\begin{array}{l}{-\sqrt{3}{m}^{2}+12\sqrt{3}m-27\sqrt{3}}&{(3<m<6)}\\{\sqrt{3}{m}^{2}-18\sqrt{3}m+81\sqrt{3}}&{(6≤m<9)}\end{array}\right.$.
(4)如图4中,
由$\left\{\begin{array}{l}{y=\sqrt{3}x-6\sqrt{3}}\\{y=-\frac{\sqrt{3}}{3}{x}^{2}+2\sqrt{3}x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=6}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=-3}\\{y=-9\sqrt{3}}\end{array}\right.$,
∴直线BC与抛物线的交点M坐标为(-3,-9$\sqrt{3}$).
观察图象可知,当△PQR与(2)中的抛物线有两个公共点时m的取值:-3<m<9.
点评 本题考查二次函数综合题、一次函数、菱形的性质、等边三角形的判定和性质,多边形的面积等知识,解题的关键是学会灵活运用所学知识解决问题,学会分类讨论,需要一定的画图能力,属于中考压轴题.

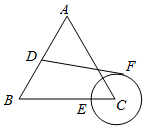 如图,等边△ABC的边长为4,D、E是边AB、BC上的动点(与A、B不重合),AD=2CE,以CE的长为半径作⊙C,DF与⊙C相切于F,下列关于DF的长说法正确的是( )
如图,等边△ABC的边长为4,D、E是边AB、BC上的动点(与A、B不重合),AD=2CE,以CE的长为半径作⊙C,DF与⊙C相切于F,下列关于DF的长说法正确的是( )| A. | 有最大值,无最小值 | B. | 有最小值,无最大值 | ||
| C. | 有最大值,也有最小值 | D. | 为定值 |
 如图:
如图: 如图,△ABC是⊙O的内接三角形,若∠OBC=70°,则∠A的度数是20°.
如图,△ABC是⊙O的内接三角形,若∠OBC=70°,则∠A的度数是20°.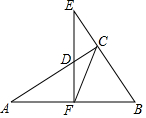 已知:如图,△ABC中,∠ACB=90°,F为AB的中点,EF⊥AB,求证:△CDF∽△ECF.
已知:如图,△ABC中,∠ACB=90°,F为AB的中点,EF⊥AB,求证:△CDF∽△ECF.