题目内容
14.已知在等腰三角形ABC中,AB=AC=10,一个底角的余弦值为$\frac{2}{5}$,那么这个等腰三角形的底边长等于10.分析 根据题意可以画出相应的图形,从而可以求得BC的长,本题得以解决.
解答  解:如右图所示,作AD⊥BC于点D,
解:如右图所示,作AD⊥BC于点D,
∵cos∠B=$\frac{2}{5}$=$\frac{BD}{AB}$,AB=AC=10,
∴BD=5,
∴BC=2BD=10,
故答案为:10.
点评 本题考查解直角三角形、等腰三角形的性质,解题的关键是明确题意,利用锐角三角函数和等腰三角形的性质解答.

练习册系列答案
相关题目
2.圆锥的底面半径为1,全面积为4π.则圆锥的母线长为( )
| A. | 4 | B. | 3 | C. | 2$\sqrt{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
17.下列运算中,正确的是( )
| A. | 22×23=26 | B. | 22×23=46 | C. | 22×23=25 | D. | 22×23=45 |
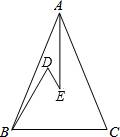 如图,已知△ABC中,AB=AC,∠DBC=∠D=60°,AE平分∠BAC,若BD=8cm,DE=3cm,则BC=11cm.
如图,已知△ABC中,AB=AC,∠DBC=∠D=60°,AE平分∠BAC,若BD=8cm,DE=3cm,则BC=11cm.