题目内容
9. △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示.(1)在网格内画出和△ABC以点O为位似中心的位似图形△A1B1C1,且△A1B1C1和△ABC的位似比为2:1;
(2)分别写出A1、B1、C1三个点的坐标:A1(4,8)或(-4,-8)、B1(2,2)或(-2,-2)、C1(8,2)或(-8,-2);
(3)求△A1B1C1的面积为18.
分析 (1)直接利用位似图形的性质得出对应点位置进而得出答案;
(2)利用(1)中所画图形得出各点坐标;
(3)利用△A1B1C1所在矩形面积,减去周围三角形面积进而得出答案.
解答 解:(1)如图所示:
△A1B1C1,即为所求;
(2)如图所示:A1 (4,8)或(-4,-8);B1 (2,2)或(-2,-2),C1(8,2)或(-8,-2);
故答案为:(4,8)或(-4,-8);(2,2)或(-2,-2),(8,2)或(-8,-2);
(3)△A1B1C1的面积为:$\frac{1}{2}$×6×6=18.
故答案是:18.
点评 此题主要考查了位似变换以及三角形面积求法,正确得出对应点位置是解题关键.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
19. 如图,在△ABC中,AB=AC,AD是BC边上中线.若AB=10,AD=8,则BC的长度是( )
如图,在△ABC中,AB=AC,AD是BC边上中线.若AB=10,AD=8,则BC的长度是( )
 如图,在△ABC中,AB=AC,AD是BC边上中线.若AB=10,AD=8,则BC的长度是( )
如图,在△ABC中,AB=AC,AD是BC边上中线.若AB=10,AD=8,则BC的长度是( )| A. | 6 | B. | 10 | C. | 12 | D. | 16 |
14. 用圆中两个可以自由转动的转盘做“配紫色”游戏,分别转动两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率是( )
用圆中两个可以自由转动的转盘做“配紫色”游戏,分别转动两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率是( )
 用圆中两个可以自由转动的转盘做“配紫色”游戏,分别转动两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率是( )
用圆中两个可以自由转动的转盘做“配紫色”游戏,分别转动两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{5}{12}$ | D. | $\frac{7}{12}$ |
1.下列关于x的方程中,一定是一元二次方程的为( )
| A. | ax2+bx+c=0 | B. | $\frac{1}{x^2}$+$\frac{1}{x}$=2 | C. | x2+2x=y2-1 | D. | 3(x+1)2=2(x+1) |
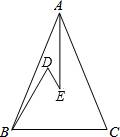 如图,已知△ABC中,AB=AC,∠DBC=∠D=60°,AE平分∠BAC,若BD=8cm,DE=3cm,则BC=11cm.
如图,已知△ABC中,AB=AC,∠DBC=∠D=60°,AE平分∠BAC,若BD=8cm,DE=3cm,则BC=11cm. 如图:
如图: