题目内容
2.对于所有有理数定义一种运算a?b=n,具有性质(a+1)?b=n+1,a?(b+1)=n-2.若有1?1=2,试求.(1)2?1=3,1?2=0.
(2)求2015?1,1?2015的值;
(3)请利用(1)(2)中的方法,求出2015?2015的值.
分析 (1)根据新定义的性质直接可得;
(2)根据性质(a+1)?b=n+1可得2015?1,根据a?(b+1)=n-2可得1?2015;
(3)在1?2015结果得基础上运用(a+1)?b=n+1可得答案.
解答 解:(1)根据题中的新定义得:2?1=(1+1)?1=2+1=3,1?2=1?(1+1)=2-2=0;
故答案为:3;0;
(2)∵1?1=2,2?1=3,3?1=4,…
∴2015?1=2016,
∵1?1=2,1?2=0,1?3=-2,1?4=-4,…
∴1?2015=-4026;
(3)∵1?2015=-4026,2?2015=-4025,3?2015=-4024,…
∴2015?2015=-2012.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
10.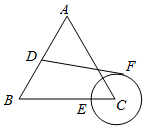 如图,等边△ABC的边长为4,D、E是边AB、BC上的动点(与A、B不重合),AD=2CE,以CE的长为半径作⊙C,DF与⊙C相切于F,下列关于DF的长说法正确的是( )
如图,等边△ABC的边长为4,D、E是边AB、BC上的动点(与A、B不重合),AD=2CE,以CE的长为半径作⊙C,DF与⊙C相切于F,下列关于DF的长说法正确的是( )
 如图,等边△ABC的边长为4,D、E是边AB、BC上的动点(与A、B不重合),AD=2CE,以CE的长为半径作⊙C,DF与⊙C相切于F,下列关于DF的长说法正确的是( )
如图,等边△ABC的边长为4,D、E是边AB、BC上的动点(与A、B不重合),AD=2CE,以CE的长为半径作⊙C,DF与⊙C相切于F,下列关于DF的长说法正确的是( )| A. | 有最大值,无最小值 | B. | 有最小值,无最大值 | ||
| C. | 有最大值,也有最小值 | D. | 为定值 |
17.下列运算中,正确的是( )
| A. | 22×23=26 | B. | 22×23=46 | C. | 22×23=25 | D. | 22×23=45 |

