题目内容
7.某花圃用花盆培育某种花苗,经试验发现每盆花的盈利与每盆花中花苗的株数有如下关系:每盆植入花苗6株时,平均单株盈利8元;以同样的栽培条件,若每盆每增加1株花苗,平均单株盈利就会减少0.5元.要使每盆花的盈利为60元,且尽可能地减少成本,则每盆花应种植花苗多少株?分析 根据题意分别表示出每盆植入的花苗株数,再表示出每株的盈利进而得出等式求出答案.
解答 解:设每盆花在植苗6株的基础上再多植x株,
由题意得:(6+x)(8-0.5x)=60,
解得:x1=6,x2=4,
因为要尽可能地减少成本,所以x2=6应舍去,
即x=4,则x+6=10,
答:每盆花植花苗10株时,每盆花的盈利为60元.
点评 此题主要考查了一元二次方程的应用,根据题意正确表示出盈利金额是解题关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
2.圆锥的底面半径为1,全面积为4π.则圆锥的母线长为( )
| A. | 4 | B. | 3 | C. | 2$\sqrt{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
10.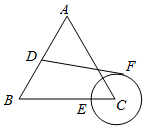 如图,等边△ABC的边长为4,D、E是边AB、BC上的动点(与A、B不重合),AD=2CE,以CE的长为半径作⊙C,DF与⊙C相切于F,下列关于DF的长说法正确的是( )
如图,等边△ABC的边长为4,D、E是边AB、BC上的动点(与A、B不重合),AD=2CE,以CE的长为半径作⊙C,DF与⊙C相切于F,下列关于DF的长说法正确的是( )
 如图,等边△ABC的边长为4,D、E是边AB、BC上的动点(与A、B不重合),AD=2CE,以CE的长为半径作⊙C,DF与⊙C相切于F,下列关于DF的长说法正确的是( )
如图,等边△ABC的边长为4,D、E是边AB、BC上的动点(与A、B不重合),AD=2CE,以CE的长为半径作⊙C,DF与⊙C相切于F,下列关于DF的长说法正确的是( )| A. | 有最大值,无最小值 | B. | 有最小值,无最大值 | ||
| C. | 有最大值,也有最小值 | D. | 为定值 |
 如图:
如图: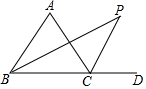 如图,△ABC的外角∠ACD的平分线:CP与内角∠ABC平分线BP交于点P,若∠A=60°,求∠P的度数.
如图,△ABC的外角∠ACD的平分线:CP与内角∠ABC平分线BP交于点P,若∠A=60°,求∠P的度数. 如图,△ABC是⊙O的内接三角形,若∠OBC=70°,则∠A的度数是20°.
如图,△ABC是⊙O的内接三角形,若∠OBC=70°,则∠A的度数是20°.