题目内容
15．若关于x的二次函数y=mx2+（1-m）x-3（其中x为正整数），若当x=4时y取得的最大值，则实数m取值范围为-$\frac{1}{6}$＜m＜-$\frac{1}{8}$．分析 根据x=4时y取得的最大值，可得不等式组，根据解不等式组，可得答案．
解答 解：由关于x的二次函数y=mx2+（1-m）x-3（其中x为正整数），若当x=4时y取得的最大值，得
$\left\{\begin{array}{l}{9m+3（1-m）-3＜16m+4（1-m）-3}\\{25m+5（1-m）-3＜16m+4（1-m）-3}\end{array}\right.$
解得-$\frac{1}{6}$＜m＜-$\frac{1}{8}$，
故答案为：-$\frac{1}{6}$＜m＜-$\frac{1}{8}$．
点评 本题考查了二次函数的最值，利用x为正整数时，x=3时和x=5时都比x=4时的y值小，得出关于m不等式组是解题关键．
练习册系列答案
相关题目
5．下列各组中的四条线段成比例的是（ ）
| A． | a=1，b=3，c=2，d=4 | B． | a=4，b=6，c=5，d=10 | ||
| C． | a=2，b=4，c=3，d=6 | D． | a=2，b=3，c=4，d=1 |
6．用火柴棒按下面的方式搭图形：
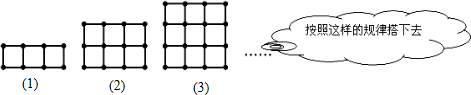
①填写下表：
②第n个图形需要多少根火柴棒？
①填写下表：
| 图形编号 | （1） | （2） | （3） | （4） | （5） | （6） |
| 火柴棒根数 | 10 | 17 | 24 | 31 | 38 | 45 |
在平面直角坐标系中，点A、B、C的坐标分别是A（-2，5），B（-3，-1），C（1，-1）找一点D，使四边形ABCD是平行四边形，求点D的坐标．
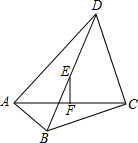已知：如图，在四边形ABCD中，∠BAD=∠BCD=90°，E，F分别是对角线BD，AC的中点．求证：EF⊥AC．
如图，Rt△ABC∽Rt△ADE，∠BCA=30°，F，M，N分别为BE，BC，DE的中点．①△BDA∽△CEA；②BD⊥CE；③∠MFN=90°；④MF=2NF．上述结论中正确的个数有（ ）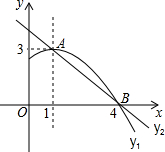
如图是抛物线y1=ax2+bx+c（a≠0）图象的一部分，抛物线的顶点坐标A（1，3），与x轴的一个交点B（4，0），直线y2=mx+n（m≠0）与抛物线交于A，B两点，下列结论：
如图，已知在△ABC中，两条内角平分线BD、CE相交于点O，若∠BOC=110°，则∠A=40度．