题目内容
10.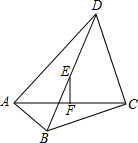 已知:如图,在四边形ABCD中,∠BAD=∠BCD=90°,E,F分别是对角线BD,AC的中点.求证:EF⊥AC.
已知:如图,在四边形ABCD中,∠BAD=∠BCD=90°,E,F分别是对角线BD,AC的中点.求证:EF⊥AC.
分析 连接AE,CE,根据直角三角形斜边上的中线等于斜边的一半可得AE=$\frac{1}{2}$BD,CE=$\frac{1}{2}$BD,那么AE=CE,再根据等腰三角形三线合一的性质即可证明EF⊥AC.
解答  证明:连接AE,CE.
证明:连接AE,CE.
∵∠BAD=∠BCD=90°,E是BD的中点,
∴AE=$\frac{1}{2}$BD,CE=$\frac{1}{2}$BD,
∴AE=CE,
又∵F是AC的中点,
∴EF⊥AC.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,熟记各性质是解题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
3.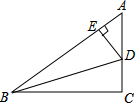 如图、已知△ABC中,∠C=90°,BD平分∠ABC,DE⊥AB于点E,且AE=3cm,AC=9cm,则△ADE的周长为( )
如图、已知△ABC中,∠C=90°,BD平分∠ABC,DE⊥AB于点E,且AE=3cm,AC=9cm,则△ADE的周长为( )
 如图、已知△ABC中,∠C=90°,BD平分∠ABC,DE⊥AB于点E,且AE=3cm,AC=9cm,则△ADE的周长为( )
如图、已知△ABC中,∠C=90°,BD平分∠ABC,DE⊥AB于点E,且AE=3cm,AC=9cm,则△ADE的周长为( )| A. | 11cm | B. | 18cm | C. | 12cm | D. | 6cm |
 如图,已知AB比AC长3cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是15cm,求AB和AC的长.
如图,已知AB比AC长3cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是15cm,求AB和AC的长.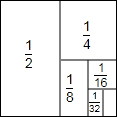 如图,把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的矩形,接着把面积为$\frac{1}{2}$的矩形等分成两个面积为$\frac{1}{4}$的矩形,再把面积为$\frac{1}{4}$的矩形等分两个面积为$\frac{1}{8}$的矩形,如此进行下去,试利用图形揭示的规律计算:
如图,把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的矩形,接着把面积为$\frac{1}{2}$的矩形等分成两个面积为$\frac{1}{4}$的矩形,再把面积为$\frac{1}{4}$的矩形等分两个面积为$\frac{1}{8}$的矩形,如此进行下去,试利用图形揭示的规律计算: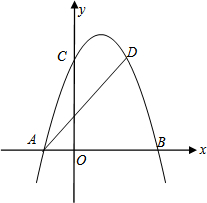 如图,已知抛物线y=-x2+2x+c与x轴交于A、B两点,与y轴交于C点,点D与点C关于抛物线的对称轴对称,点A的坐标为(-1,0).
如图,已知抛物线y=-x2+2x+c与x轴交于A、B两点,与y轴交于C点,点D与点C关于抛物线的对称轴对称,点A的坐标为(-1,0). 如图,△ABC中,BD是角平分线,过D作DE∥AB交BC于点E,AB=5cm,BE=3cm,分别求出DE与EC的长.
如图,△ABC中,BD是角平分线,过D作DE∥AB交BC于点E,AB=5cm,BE=3cm,分别求出DE与EC的长.