题目内容
8. 如图,已知在△ABC中,两条内角平分线BD、CE相交于点O,若∠BOC=110°,则∠A=40度.
如图,已知在△ABC中,两条内角平分线BD、CE相交于点O,若∠BOC=110°,则∠A=40度.
分析 根据三角形内角和定理易得∠OBC+∠OCB=70°,利用角平分线定义可得∠ABC+∠ACB=2(∠OBC+∠OCB)=140°,进而利用三角形内角和定理可得∠A度数.
解答 解:∵∠BOC=110°,
∴∠OBC+∠OCB=180°-11°=70°.
∵∠ABC与∠ACB的平分线相交于O点,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴∠ABC+∠ACB=2(∠OBC+∠OCB)=140°,
∴∠A=180°-140°=40°.
故答案为:40.
点评 本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
相关题目
16.在3.14,0.1010010…,π,$\sqrt{9}$,$\frac{\sqrt{2}}{2}$,-$\frac{22}{7}$,-$\root{3}{4}$这些实数中无理数有( )个.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
3.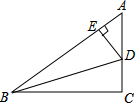 如图、已知△ABC中,∠C=90°,BD平分∠ABC,DE⊥AB于点E,且AE=3cm,AC=9cm,则△ADE的周长为( )
如图、已知△ABC中,∠C=90°,BD平分∠ABC,DE⊥AB于点E,且AE=3cm,AC=9cm,则△ADE的周长为( )
 如图、已知△ABC中,∠C=90°,BD平分∠ABC,DE⊥AB于点E,且AE=3cm,AC=9cm,则△ADE的周长为( )
如图、已知△ABC中,∠C=90°,BD平分∠ABC,DE⊥AB于点E,且AE=3cm,AC=9cm,则△ADE的周长为( )| A. | 11cm | B. | 18cm | C. | 12cm | D. | 6cm |
13. 如图,已知AB⊥BD,AC⊥CD,∠A=40°,则∠D的度数为( )
如图,已知AB⊥BD,AC⊥CD,∠A=40°,则∠D的度数为( )
 如图,已知AB⊥BD,AC⊥CD,∠A=40°,则∠D的度数为( )
如图,已知AB⊥BD,AC⊥CD,∠A=40°,则∠D的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
 如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2.
如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2.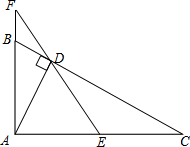 如图,已知∠BAC=90°,AD⊥BC于D,E是AC的中点,ED的延长线交AB的延长线于点F.求证:
如图,已知∠BAC=90°,AD⊥BC于D,E是AC的中点,ED的延长线交AB的延长线于点F.求证: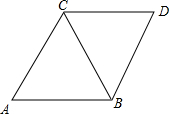 已知:如图,等边三角形ABC与等边三角形DBC的一边BC重合
已知:如图,等边三角形ABC与等边三角形DBC的一边BC重合