题目内容
10.解下列方程组:(1)$\left\{\begin{array}{l}{4x-3y=17}\\{y=7-5x}\end{array}\right.$
(2)$\left\{\begin{array}{l}{3x+2y=14}\\{x-y=3}\end{array}\right.$
(3)$\left\{\begin{array}{l}{5x-y=5}\\{y=\frac{1}{5}x}\end{array}\right.$.
分析 (1)此方程采用代入消元法最简单,可以直接把②代入①,即可消去未知数y,解方程即可求得.
(2)先用加减消元法求出x的值,再用代入消元法求出y的值即可.
(3)此方程采用代入消元法最简单,可以直接把②代入①,即可消去未知数y,解方程即可求得.
解答 解:(1)在$\left\{\begin{array}{l}{4x-3y=17①}\\{y=7-5x②}\end{array}\right.$中,
把②代入①得:4x-3(7-5x)=17,
∴4x-21+15x=17,
∴19x=38,
∴x=2,
把x=2代入②得:x=-3.
∴原方程组的解是$\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$.
(2)$\left\{\begin{array}{l}{3x+2y=14①}\\{x-y=3②}\end{array}\right.$,
①+②×2得,5x=20,解得x=4,
把x=4代入②得,4-y=3,解得y=1,
故方程组的解为$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$.
(3)$\left\{\begin{array}{l}{5x-y=5①}\\{y=\frac{1}{5}x②}\end{array}\right.$
把②代入①得5x-$\frac{1}{5}$x=5,
∴24x=25,
∴x=$\frac{25}{24}$,
把x=$\frac{25}{24}$代入②得:y=$\frac{5}{24}$.
∴原方程组的解是$\left\{\begin{array}{l}{x=\frac{25}{24}}\\{y=\frac{5}{24}}\end{array}\right.$.
点评 本题考查的是解二元一次方程组,熟知解二元一次方程组的加减消元法和代入消元法是解答此题的关键.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案| A. | 如果ax=bx,那么a=b | B. | 如果a=b,那么$\frac{a}{{c}^{2}+1}$=$\frac{b}{{c}^{2}+1}$ | ||
| C. | 如果a=b,那么ac-d=bc-d | D. | 如果x=3,那么x2=3x |
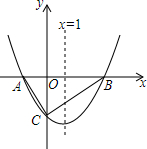 对称轴x=1的抛物线y=x2+bx+c与x轴交于点A、B,其中点A(-1,0)
对称轴x=1的抛物线y=x2+bx+c与x轴交于点A、B,其中点A(-1,0)