题目内容
分别以Rt△ABC的三边为直径作半圆
(1)若这三个半圆在BC的两侧(如图甲所示),半圆的面积分别为S1,S2,S3 那么:S1、S2、S3之间有什么数量关系?请说明理由.
(2)若这三个半圆在BC的同一侧(如图乙所示)Rt△ABC的面积等于S3,两个“月牙”的面积部分别为S1、S2那么:S1、S2、S3之间有什么数量关系?请说明理由.
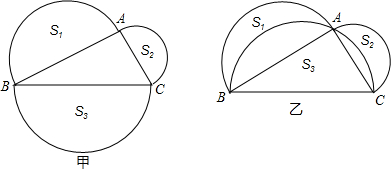
(1)若这三个半圆在BC的两侧(如图甲所示),半圆的面积分别为S1,S2,S3 那么:S1、S2、S3之间有什么数量关系?请说明理由.
(2)若这三个半圆在BC的同一侧(如图乙所示)Rt△ABC的面积等于S3,两个“月牙”的面积部分别为S1、S2那么:S1、S2、S3之间有什么数量关系?请说明理由.

考点:勾股定理
专题:计算题
分析:(1)S1+S2=S3,理由为:根据圆的面积公式表示出S1、S2、S3,利用勾股定理列出关系式,整理即可得证;
(2)S1+S2=S3,同理可证.
(2)S1+S2=S3,同理可证.
解答:解:(1)S1+S2=S3,理由为:
由题意得:S1=
π(
)2=
πc2,S2=
π(
)2=
πb2,S3=
π(
)2=
πa2,
在Rt△ABC中,根据勾股定理得:BC2=AB2+AC2,即b2+c2=a2,
∴
πc2+
πb2=
πa2,
则S1+S2=S3;
(2)S1+S2=S3,同理可证.
由题意得:S1=
| 1 |
| 2 |
| c |
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
| b |
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
| a |
| 2 |
| 1 |
| 8 |
在Rt△ABC中,根据勾股定理得:BC2=AB2+AC2,即b2+c2=a2,
∴
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
则S1+S2=S3;
(2)S1+S2=S3,同理可证.
点评:此题考查了勾股定理,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
两个三角形有两边和一角对应相等,则两个三角形( )
| A、一定全等 |
| B、一定不全等 |
| C、可能全等,可能不全等 |
| D、以上都不是 |
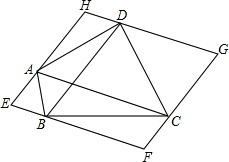 如图,过四边形ABCD的四个顶点分别作对角线AC、BD的平行线,所围成的四边形EFGH显然是平行四边形.
如图,过四边形ABCD的四个顶点分别作对角线AC、BD的平行线,所围成的四边形EFGH显然是平行四边形.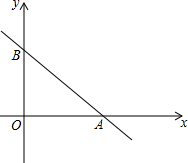 如图,直线y=-
如图,直线y=- 如图,在三角形ABC中,BC=10cm,若A点到BC的距离AF=8cm,则三角形ABC的面积为
如图,在三角形ABC中,BC=10cm,若A点到BC的距离AF=8cm,则三角形ABC的面积为