题目内容
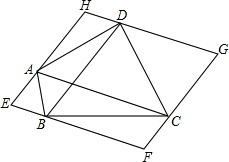 如图,过四边形ABCD的四个顶点分别作对角线AC、BD的平行线,所围成的四边形EFGH显然是平行四边形.
如图,过四边形ABCD的四个顶点分别作对角线AC、BD的平行线,所围成的四边形EFGH显然是平行四边形.(1)当四边形ABCD是分别菱形、矩形时,相应的平行四边形EFGH一定是“菱形、矩形、正方形”中的哪一种?请将你的结论填入下表:
| 四边形ABCD | 菱形 | 矩形 |
| 平行四边形EFGH |
(3)反之,当用上述方法所围成的平行四边形是矩形时,相应的原四边形必须满足怎样的条件?(直接写出结论)
考点:矩形的判定,平行四边形的判定,菱形的判定
专题:
分析:(1)原四边形是菱形时,菱形的对角线互相垂直,因此平行四边形应该是个矩形(平行四边形相邻的两边都垂直),
原四边形是矩形时,它的对角线相等,那么平行四边形应该是个菱形(平行四边形相邻的两边都相等);
(2)根据平行公理的推论求出EF∥GH,EH∥FG,推出平行四边形EFGH,证出邻边相等即可;
(3)根据(1)我们可看出要想使得出的平行四边形是矩形,那么原四边形的对角线就必须垂直,因为只有这样平行四边形的相邻两边才垂直.
原四边形是矩形时,它的对角线相等,那么平行四边形应该是个菱形(平行四边形相邻的两边都相等);
(2)根据平行公理的推论求出EF∥GH,EH∥FG,推出平行四边形EFGH,证出邻边相等即可;
(3)根据(1)我们可看出要想使得出的平行四边形是矩形,那么原四边形的对角线就必须垂直,因为只有这样平行四边形的相邻两边才垂直.
解答:解:(1)四边形ABCD是菱形时,平行四边形EFGH是矩形,
四边形ABCD是矩形时,平行四边形EFGH是菱形,
故答案为:矩形,菱形.
(2)如图所示:
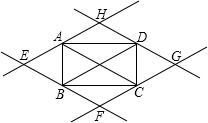
当四边形ABCD是矩形时,平行四边形EFGH是矩形;
理由:∵EF∥AC∥HG,EH∥BD∥GF.
∴四边形EAOB,EFGH均为平行四边形,
∵四边形ABCD为矩形,
∴AC=DB,
∴EH=EF=FG=HG,
∴四边形EFGH为菱形;
(3)当平行四边形是矩形时,原四边形ABCD必须满足的条件是对角线互相垂直.
四边形ABCD是矩形时,平行四边形EFGH是菱形,
故答案为:矩形,菱形.
(2)如图所示:

当四边形ABCD是矩形时,平行四边形EFGH是矩形;
理由:∵EF∥AC∥HG,EH∥BD∥GF.
∴四边形EAOB,EFGH均为平行四边形,
∵四边形ABCD为矩形,
∴AC=DB,
∴EH=EF=FG=HG,
∴四边形EFGH为菱形;
(3)当平行四边形是矩形时,原四边形ABCD必须满足的条件是对角线互相垂直.
点评:本题主要考查了矩形的性质和判定,菱形的性质和判定等知识点.能求出平行四边形EFHG是解此题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
已知△ABC,∠A=40°,∠C=90°,AB=8,则AC=( )
| A、8cos40° |
| B、8sin40° |
| C、8cos30° |
| D、8tan40° |
 已知,如图,AB是⊙O的直径,CD是⊙O的弦,且AB⊥CD,垂足为E.
已知,如图,AB是⊙O的直径,CD是⊙O的弦,且AB⊥CD,垂足为E.
 如图,AC⊥EC,B,C,D在同一直线上,∠A=∠1,∠E=∠2,直线AB与DE平行吗?试说明理由.
如图,AC⊥EC,B,C,D在同一直线上,∠A=∠1,∠E=∠2,直线AB与DE平行吗?试说明理由.