题目内容
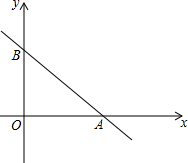 如图,直线y=-
如图,直线y=-| 3 |
| 4 |
考点:一次函数图象上点的坐标特征,等腰直角三角形
专题:
分析:分三种情况分别讨论求得;①当∠PAB=90°时,过P作PD⊥x轴于D,通过△ABO≌△PAD即可求得;②当∠PBA=90°时,过P作PE⊥y轴于E,通过△ABO≌△BPE即可求得;③当∠APB=90°时,过P作PG⊥x轴,过B作BH⊥PG,通过△PBH≌△APG即可求得;
解答:解:存在点P.理由如下:
∵直线y=-
x+3与x轴、y轴分别交于点A,点B,
∴A(4,0),B(0,3);
①当∠PAB=90°时,过P作PD⊥x轴于D,如图1,
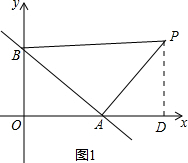
∵∠ABO+∠OAB=90°,∠PAD+∠OAB=90°,
∴∠ABO=∠PAD,
在△ABO和△PAD中,
,
∴△ABO≌△PAD(AAS),
∴AD=OB,PD=OA,
∴OD=OA+OB=4+3=7,PD=4,
∴P的坐标为(7,4);
②当∠PBA=90°时,过P作PE⊥y轴于E,如图2,
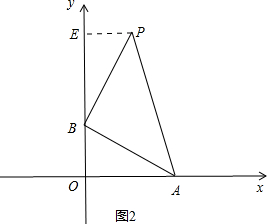
同理可证△ABO≌△BPE,
∴BE=OA.PE=OB,
∴OE=OB+BE=3+4=7,PE=3,
∴P的坐标为(3,7);
③当∠APB=90°时,如图3,过P作PG⊥x轴,过B作BH⊥PG,
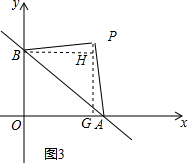
∵△PAB为等腰直角三角形,
∴PA=PB,∠APB=90°,
∴∠BPH+∠APG=90°,
∵∠BPH+∠PBH=90°,
∴∠APG=∠PBH,
在△PBH和△APG中,
,
∴△PBH≌△APG(AAS),
∴BH=PG,PH=GA,
设BH=PG=x,PH=GA=y,
则x+y=4,x-y=3,
解得x=
,y=
,
∴P的坐标为(
,
).
综上,P的坐标为(7,4)或(3,7)或(
,
);
∵直线y=-
| 3 |
| 4 |
∴A(4,0),B(0,3);
①当∠PAB=90°时,过P作PD⊥x轴于D,如图1,

∵∠ABO+∠OAB=90°,∠PAD+∠OAB=90°,
∴∠ABO=∠PAD,
在△ABO和△PAD中,
|
∴△ABO≌△PAD(AAS),
∴AD=OB,PD=OA,
∴OD=OA+OB=4+3=7,PD=4,
∴P的坐标为(7,4);
②当∠PBA=90°时,过P作PE⊥y轴于E,如图2,

同理可证△ABO≌△BPE,
∴BE=OA.PE=OB,
∴OE=OB+BE=3+4=7,PE=3,
∴P的坐标为(3,7);
③当∠APB=90°时,如图3,过P作PG⊥x轴,过B作BH⊥PG,

∵△PAB为等腰直角三角形,
∴PA=PB,∠APB=90°,
∴∠BPH+∠APG=90°,
∵∠BPH+∠PBH=90°,
∴∠APG=∠PBH,
在△PBH和△APG中,
|
∴△PBH≌△APG(AAS),
∴BH=PG,PH=GA,
设BH=PG=x,PH=GA=y,
则x+y=4,x-y=3,
解得x=
| 7 |
| 2 |
| 1 |
| 2 |
∴P的坐标为(
| 7 |
| 2 |
| 7 |
| 2 |
综上,P的坐标为(7,4)或(3,7)或(
| 7 |
| 2 |
| 7 |
| 2 |
点评:此题属于一次函数综合题,涉及的知识有:一次函数与坐标轴的交点,全等三角形的判定与性质,等腰直角三角形的性质,坐标与图形性质,作出辅助线构建全等三角形是解本题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
已知△ABC,∠A=40°,∠C=90°,AB=8,则AC=( )
| A、8cos40° |
| B、8sin40° |
| C、8cos30° |
| D、8tan40° |
 已知,如图,AB是⊙O的直径,CD是⊙O的弦,且AB⊥CD,垂足为E.
已知,如图,AB是⊙O的直径,CD是⊙O的弦,且AB⊥CD,垂足为E.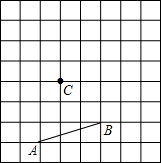 如图,请按要求作图,并回答问题:
如图,请按要求作图,并回答问题: