题目内容
阅读材料:据统计,某市2012年上半年空气质量达到优秀和良好的天数共176天,比2011年上半年增加了16天,其中空气质量达到优秀的天数比2011年上半年增加40%,空气质量达到良好的天数比2011年上半年减少20%.
解答问题:
(1)该市2011年上半年空气质量达到优秀和良好的天数有 天.
(2)若该市2011年上半年空气质量达到优秀的天数为x天,则2012年上半年该市空气质量达到优秀的天数有 天.(用含x的代数式表示)
(3)求该市2012年上半年空气质量达到优秀和良好的天数分别有多少天?
解答问题:
(1)该市2011年上半年空气质量达到优秀和良好的天数有
(2)若该市2011年上半年空气质量达到优秀的天数为x天,则2012年上半年该市空气质量达到优秀的天数有
(3)求该市2012年上半年空气质量达到优秀和良好的天数分别有多少天?
考点:一元一次方程的应用
专题:
分析:(1)由2012年上半年空气质量达到优秀和良好的天数共176天,比2011年上半年增加了16天,直接列式计算即可;
(2)根据空气质量达到优秀的天数比2011年上半年增加40%,得出2012年上半年该市空气质量达到优秀的天数有x+40%x=1.4x天;
(3)再进一步用x表示出2012年上半年空气质量达到良好的天数,列出方程解决问题.
(2)根据空气质量达到优秀的天数比2011年上半年增加40%,得出2012年上半年该市空气质量达到优秀的天数有x+40%x=1.4x天;
(3)再进一步用x表示出2012年上半年空气质量达到良好的天数,列出方程解决问题.
解答:解:(1)该市2011年上半年空气质量达到优秀和良好的天数有176-16=160天.
(2)若该市2011年上半年空气质量达到优秀的天数为x天,则2012年上半年该市空气质量达到优秀的天数有x+40%x=1.4x天.
(3)出2012年上半年空气质量达到良好的天数为(160-x)(1-20%),由题意得
1.4x+(160-x)(1-20%)=176
解得:x=80
则1.4x=112天,(160-x)(1-20%)=64天
答:2012年上半年空气质量达到优秀的天数有112天;2012年上半年空气质量达到良好的天数为64天.
(2)若该市2011年上半年空气质量达到优秀的天数为x天,则2012年上半年该市空气质量达到优秀的天数有x+40%x=1.4x天.
(3)出2012年上半年空气质量达到良好的天数为(160-x)(1-20%),由题意得
1.4x+(160-x)(1-20%)=176
解得:x=80
则1.4x=112天,(160-x)(1-20%)=64天
答:2012年上半年空气质量达到优秀的天数有112天;2012年上半年空气质量达到良好的天数为64天.
点评:此题考查一元一次方程的实际运用,理解题意,找出题目蕴含的数量关系是解决问题的关键.

练习册系列答案
相关题目
已知△ABC,∠A=40°,∠C=90°,AB=8,则AC=( )
| A、8cos40° |
| B、8sin40° |
| C、8cos30° |
| D、8tan40° |
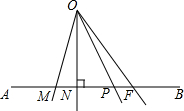 如图,过直线AB外一点O,画射线OM,ON,OP,OF,分别交AB于点M,N,P,F,其中ON⊥AB于点N,则能表示点O到直线AB的距离的是线段
如图,过直线AB外一点O,画射线OM,ON,OP,OF,分别交AB于点M,N,P,F,其中ON⊥AB于点N,则能表示点O到直线AB的距离的是线段 如图,AC⊥EC,B,C,D在同一直线上,∠A=∠1,∠E=∠2,直线AB与DE平行吗?试说明理由.
如图,AC⊥EC,B,C,D在同一直线上,∠A=∠1,∠E=∠2,直线AB与DE平行吗?试说明理由.