题目内容
18.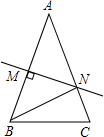 如图,在三角形ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交AB于点M,交AC于点N,下面结论:①BN平分∠ABC;②△BCN是等腰三角形;③△BMN≌△BCN;④△BCN的周长等于AB+BC,其中正确的结论是( )
如图,在三角形ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交AB于点M,交AC于点N,下面结论:①BN平分∠ABC;②△BCN是等腰三角形;③△BMN≌△BCN;④△BCN的周长等于AB+BC,其中正确的结论是( )| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
分析 根据等腰三角形的性质求出∠ABC和∠ACB的度数,根据线段垂直平分线的性质证明NB=NA,进行判断即可.
解答 解:∵AB=AC,∠A=36°,
∴∠ABC=∠ACB=72°,
∵MN是AB的垂直平分线,
∴NB=NA,∴∠NBA=∠A=36°,
∴∠NBC=∠ABC-∠NBC=36°,
∴BN平分∠ABC,①正确;
∠BNC=∠A+∠NBC=72°,
∴∠BNC=∠ACB,
∴△BCN是等腰三角形,②正确;
△BMN是直角三角形,△BCN是锐角三角形,∴△BMN≌△BCN不正确,③错误;
△BCN的周长等于BN+CN+BC=AN+CN+BC=AC+BC=AB+BC,④正确,
故选:B.
点评 本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
7.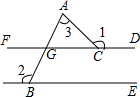 如图,已知FD∥BE,则∠1+∠2-∠3的值为( )
如图,已知FD∥BE,则∠1+∠2-∠3的值为( )
 如图,已知FD∥BE,则∠1+∠2-∠3的值为( )
如图,已知FD∥BE,则∠1+∠2-∠3的值为( )| A. | 90° | B. | 135° | C. | 150° | D. | 180° |
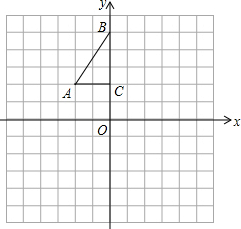 如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点分别为A(-2,2),B(0,5),C(0,2).
如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点分别为A(-2,2),B(0,5),C(0,2).
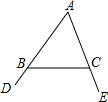 我们知道,三角形的一个外角等于与它不相邻的两个内角的和,那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
我们知道,三角形的一个外角等于与它不相邻的两个内角的和,那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?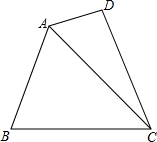 如图,在四边形ABCD中,AC平分∠BAD,且AC=BC,AB=2AD.
如图,在四边形ABCD中,AC平分∠BAD,且AC=BC,AB=2AD.