题目内容
8.若y与x-1成正比例,x=8时,y=6,写出x与y之间的函数关系式,并分别求出x=4和x=-3时的值.分析 根据正比例函数定义,设y=k(x-1),把x=8,y=6代入求出k的值,从而得到x与y之间的函数关系式,然后分别计算出x=4和x=-3所对应的y的值.
解答 解:设y=k(x-1),
把x=8,y=6代入得k×(8-1)=6,解得k=$\frac{6}{7}$,
所以y=$\frac{6}{7}$(x-1)=$\frac{6}{7}$x-$\frac{6}{7}$,
所以x=$\frac{7}{6}$y+1,
当x=4时,y=$\frac{6}{7}$×4-$\frac{6}{7}$=$\frac{18}{7}$;
当x=-3时,y=$\frac{6}{7}$×(-3)-$\frac{6}{7}$=-$\frac{24}{7}$.
点评 本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b,再将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组,然后解方程或方程组,求出待定系数的值,进而写出函数解析式.

练习册系列答案
相关题目
18.融侨半岛某文具店购入一批笔袋进行销售,进价为每个20元,当售价为每个50元时,每星期可以卖出100个,现需降价处理:售价每降价3元,每星期可以多卖出15个,店里每星期笔袋的利润要达到3125元.若设店主把每个笔袋售价降低x元,则可列方程为( )
| A. | (30+x)(100-15x)=3125 | B. | (30-x)(100+15x)=3125 | ||
| C. | (30+x)(100-5x)=3125 | D. | (30-x)(100+5x)=3125 |
19.若关于x的不等式组$\left\{\begin{array}{l}{x>a}\\{3x+1<4x-3}\end{array}\right.$的解集是x>4,则a的取值范围是( )
| A. | a≤4 | B. | a>4 | C. | a<4 | D. | a≥4 |
3.下列关于概率的描述属于“等可能性事件”的是( )
| A. | 交通信号灯有“红、绿、黄”三种颜色,它们发生的概率 | |
| B. | 掷一枚图钉,落地后钉尖“朝上”或“朝下”的概率 | |
| C. | 小亮在沿着“直角三角形”三边的小路上散步,他出现在各边上的概率 | |
| D. | 小明用随机抽签的方式选择以上三种答案,则A、B、C被选中的概率 |
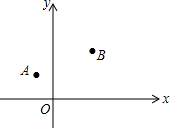 如图所示,x轴所在直线是一条东西走向的河,A(-2,3)、B(4,5)两个村庄位于河的北岸,现准备在河上修建一净水站P,并利用管道为两个村庄供水(单位:千米).
如图所示,x轴所在直线是一条东西走向的河,A(-2,3)、B(4,5)两个村庄位于河的北岸,现准备在河上修建一净水站P,并利用管道为两个村庄供水(单位:千米).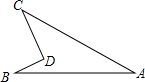 如图,∠BDC=98°,∠ACD=38°,∠ABD=23°,则∠A的度数是37°.
如图,∠BDC=98°,∠ACD=38°,∠ABD=23°,则∠A的度数是37°.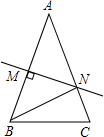 如图,在三角形ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交AB于点M,交AC于点N,下面结论:①BN平分∠ABC;②△BCN是等腰三角形;③△BMN≌△BCN;④△BCN的周长等于AB+BC,其中正确的结论是( )
如图,在三角形ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交AB于点M,交AC于点N,下面结论:①BN平分∠ABC;②△BCN是等腰三角形;③△BMN≌△BCN;④△BCN的周长等于AB+BC,其中正确的结论是( )