题目内容
14.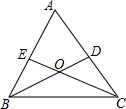 如图,△ABC中,BD、CE是△ABC的角平分线,若∠A=70°,求∠BOC的度数.
如图,△ABC中,BD、CE是△ABC的角平分线,若∠A=70°,求∠BOC的度数.
分析 由于∠A=70°,根据三角形的内角和定理,得∠ABC与∠ACB的度数和,再由角平分线的定义,得∠OBC+∠OCB的度数,进而求出∠BOC的度数.
解答 解:∵∠A=70°,
∴∠ABC+∠ACB=180°-70°=110°,
∵BE、CF是△ABC的角平分线,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=55°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-55°=125°.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.在△ABC中,AB=3,BC=4,若△ABC是直角形,则AC的长应是( )
| A. | 5 | B. | $\sqrt{7}$ | C. | 5或$\sqrt{7}$ | D. | 5或$\sqrt{8}$ |
6.圆上有两点A,B,劣弧AB的度数为120°,那么,优弧AB所对的圆心角的度数为( )
| A. | 80° | B. | 120° | C. | 180° | D. | 240° |
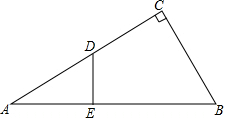 在△ABC中,∠ACB=90°,DE⊥AB,
在△ABC中,∠ACB=90°,DE⊥AB, 如图,直线a,b被直线c,d所截,若∠1=112°,∠2=68°,∠3=100°,则∠4=100°.
如图,直线a,b被直线c,d所截,若∠1=112°,∠2=68°,∠3=100°,则∠4=100°.
 方格中,除9和-2外其余字母各表示一个数,已知方格中任意三个连续方格中的数之和为19,求A+H+M+N的值.
方格中,除9和-2外其余字母各表示一个数,已知方格中任意三个连续方格中的数之和为19,求A+H+M+N的值. 如图所示,求∠1的大小.
如图所示,求∠1的大小.