题目内容
18.乘法公式的探究及应用.(1)如图1可以求出阴影部分的面积是a2-b2(写成两数平方差的形式);
(2)如图2若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是a-b,长是a+b,面积是(a+b)(a-b)(写成多项式乘法的形式);
(3)比较图1、图2两图的阴影部分面积,可以得到乘法公式(a+b)(a-b)=a2-b2 (用式子表达);
(4)运用你所得到的公式,计算下列各题:
①(2m+n-p)(2m-n+p)
②10.3×9.7.
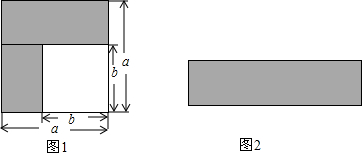
分析 (1)利用正方形的面积公式就可求出;
(2)仔细观察图形就会知道长,宽,由面积公式就可求出面积;
(3)建立等式就可得出;
(4)利用平方差公式就可方便简单的计算.
解答 解:(1)利用正方形的面积公式可知:阴影部分的面积=a2-b2;
故答案为:a2-b2;
(2)由图可知矩形的宽是a-b,长是a+b,所以面积是(a+b)(a-b);
故答案为:a-b,a+b,(a+b)(a-b);
(3)(a+b)(a-b)=a2-b2(等式两边交换位置也可);
故答案为:(a+b)(a-b)=a2-b2;
(4)①原式=[2m+(n-p)]•[2m-(n-p)]
=(2m)2-(n-p)2
=4m2-n2+2np-p2;
②原式=(10+0.3)×(10-0.3)
=102-0.32
=100-0.09
=99.91.
点评 此题主要考查了平方差公式.即两个数的和与这两个数的差的积等于这两个数的平方差,这个公式就叫做平方差公式.对于有图形的题同学们注意利用数形结合求解更形象直观.

练习册系列答案
相关题目
9.若关于x的方程x2-2x+a=3的解为x=-2,则字母a的值为( )
| A. | 3 | B. | 5 | C. | -5 | D. | 11 |
6.如果一个角的两边分别平行于另一个角的两边,那么这两个角( )
| A. | 相等 | B. | 互补 | C. | 相等或互补 | D. | 无法确定 |
10. 如图,DE∥BC,AD:DB=1:2,则△ADE和△ABC的相似比为( )
如图,DE∥BC,AD:DB=1:2,则△ADE和△ABC的相似比为( )
 如图,DE∥BC,AD:DB=1:2,则△ADE和△ABC的相似比为( )
如图,DE∥BC,AD:DB=1:2,则△ADE和△ABC的相似比为( )| A. | 1:2 | B. | 1:3 | C. | 2:1 | D. | 2:3 |
 甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题: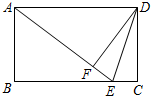 如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=3,BE:EC=4:1,则线段DE的长为$\sqrt{10}$.
如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=3,BE:EC=4:1,则线段DE的长为$\sqrt{10}$.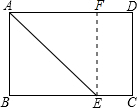 如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点F处,折痕与边BC交于点E,则CE的长为2cm.
如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点F处,折痕与边BC交于点E,则CE的长为2cm.