题目内容
17.将抛物线C1:y=$\frac{1}{9}$(x+t)2-2绕原点旋转180°,得到抛物线C2,若抛物线C1的顶点在抛物线C2上,求抛物线C2的函数表达式.分析 当抛物线C1:y=$\frac{1}{9}$(x+t)2-2绕原点旋转180°后抛物线的顶点坐标为(t,2),并且开口方向相反,于是根据顶点式写出旋转后的抛物线C2的解析式.把抛物线C1的顶点坐标代入抛物线C2的函数表达式即可求得t的值.
解答 解:∵y=$\frac{1}{9}$(x+t)2-2的顶点坐标为(-t,-2),
∴抛物线C1绕原点旋转180°,得到抛物线C2顶点坐标为(t,2),
∴抛物线C2的解析式为y=-$\frac{1}{9}$(x-t)2+2,
∵抛物线C1的顶点在抛物线C2上,
-$\frac{1}{9}$(-t-t)2+2=-2,
解得t1=3,t2=-3.
∴抛物线C2的解析式为y=-$\frac{1}{9}$(x-3)2+2或y=-$\frac{1}{9}$(x+3)2+2.
点评 本题考查了二次函数图象与几何变换,难度较大,求出旋转后的抛物线C2的顶点坐标是解题的关键,也是本题的难点.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 如图,△MNK和△ACB都是等腰直角三角形,M为AB的中点,AC=BC=4.若AD=1,求重叠部分图形的周长.
如图,△MNK和△ACB都是等腰直角三角形,M为AB的中点,AC=BC=4.若AD=1,求重叠部分图形的周长.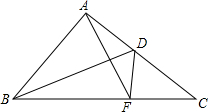 已知:在△ABC中,AB=AC,∠BAC=90°,D为AC的中点,F为BC上一点,且∠ADB=∠CDF,连接AF.求证:AF⊥BD.
已知:在△ABC中,AB=AC,∠BAC=90°,D为AC的中点,F为BC上一点,且∠ADB=∠CDF,连接AF.求证:AF⊥BD.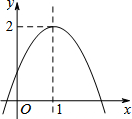 二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论: