题目内容
7．在△ABC中，AB=5，BC=6，B为锐角且sinB=$\frac{3}{5}$，则∠C的正切值等于$\frac{3}{2}$．分析 作AD⊥BC于D，根据sinB=$\frac{3}{5}$，AB=5和三角函数的概念求出DA的长，根据勾股定理求出BD的长，求出CD的长，根据正切的概念求出∠C的正切值．
解答 
解：作AD⊥BC于D，
∵sinB=$\frac{3}{5}$，AB=5，
∴AD=3，由勾股定理得，BD=4，
∴CD=2，
∴tanC=$\frac{AD}{CD}$=$\frac{3}{2}$，
故答案为：$\frac{3}{2}$．
点评 本题考查的是解直角三角形知识的运用，掌握锐角三角函数的概念是解题的关键．
练习册系列答案
相关题目
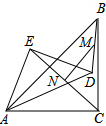已知等腰Rt△ABC和等腰Rt△ABC中，∠ACB=∠AED=90°，且AD=AC，若点M、N分别是DB、EC的中点，证明：MN⊥EC，MN=$\frac{1}{2}$EC．
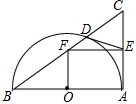如图，以Rt△ABC的直角边AB为直径作半圆⊙O与边BC交于点D，过D作半圆的切线与边AC交于点E，过E作EF∥AB，与BC交于点F．若AB=20，OF=7.5，则CD的长为（ ）
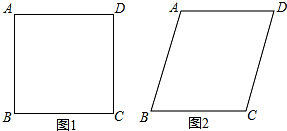将四根长度相等的细木条首尾相接，用钉子钉成四边形ABCD，转动这个四边形，使它形状改变，当∠B=90°时，如图1，测得AC=2，当∠B=60°时，如图2，AC=$\sqrt{2}$．
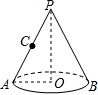小明在圣诞节前做了一顶圆锥形纸帽PAB（如图），底面周长=14πcm，母线PA=28cm，一根彩带从母线PA的中点C开始绕圆锥形纸帽PAB的侧面到A点，则彩带长至少需14$\sqrt{5}$cm．