题目内容
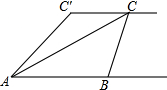 如图,小敏、小亮从A,B两地观测空中C处一个气球,分别测得仰角为30°和60°,A,B两地相距100 米.当气球沿与BA平行地飘移10秒后到达C′处时,在A处测得气球的仰角为45°.
如图,小敏、小亮从A,B两地观测空中C处一个气球,分别测得仰角为30°和60°,A,B两地相距100 米.当气球沿与BA平行地飘移10秒后到达C′处时,在A处测得气球的仰角为45°.(1)求气球的高度;
(2)气球飘移的平均速度是每秒多少米?
( 以上两小题的结果都保留根式 )
考点:解直角三角形的应用-仰角俯角问题
专题:
分析:(1)分别过C、C′作AB的垂线,设垂足为D、E;在Rt△ACD和Rt△BCD中,利用所给角的三角函数分别用BD表示出CD,联立两式即可求出CD、BD的长.
(2)直角梯形ADCC′中,已知了BD、AB的长,即可求出AD的长;而AE的长可在Rt△ABC′中利用已知角的三角函数求出,即可得出ED、CC′的长,也就得出了气球10秒漂移的距离,根据速度=路程÷时间,即可得解.
(2)直角梯形ADCC′中,已知了BD、AB的长,即可求出AD的长;而AE的长可在Rt△ABC′中利用已知角的三角函数求出,即可得出ED、CC′的长,也就得出了气球10秒漂移的距离,根据速度=路程÷时间,即可得解.
解答:解:(1)作CD⊥AB,C′E⊥AB,垂足分别为D,E.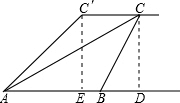
∵CD=BD•tan60°,
CD=(100+BD)•tan30°,
∴(100+BD)•tan30°=BD•tan60°,
∴BD=50m,CD=50
m.
∴气球的高度约为50
m;
(2)∵BD=50m,AB=100m,
∴AD=150m.
又∵AE=C′E=50
m,
∴DE=150-50
(m).
∴气球飘移的平均速度约为(150-50
)÷10=15-5
(米/秒).

∵CD=BD•tan60°,
CD=(100+BD)•tan30°,
∴(100+BD)•tan30°=BD•tan60°,
∴BD=50m,CD=50
| 3 |
∴气球的高度约为50
| 3 |
(2)∵BD=50m,AB=100m,
∴AD=150m.
又∵AE=C′E=50
| 3 |
∴DE=150-50
| 3 |
∴气球飘移的平均速度约为(150-50
| 3 |
| 3 |
点评:本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.解直角梯形可以通过作高线转化为解直角三角形和矩形的问题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
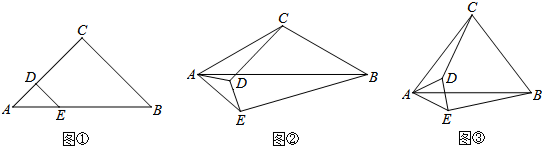
 如图,画出△OAB向下平移4个单位长度、再向左平移2个单位长度后的△O1A1B1.
如图,画出△OAB向下平移4个单位长度、再向左平移2个单位长度后的△O1A1B1.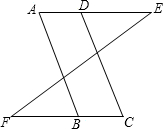 如图,在:①AB∥CD;②AD∥BC;③∠A=∠C中,请你选取其中的两个作为条件,另一个作为结论,写出一个正确命题,并证明其正确性.
如图,在:①AB∥CD;②AD∥BC;③∠A=∠C中,请你选取其中的两个作为条件,另一个作为结论,写出一个正确命题,并证明其正确性.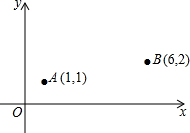 已知A(1,1),B(6,2),C、D分别为x轴、y轴上的动点,在运动的过程中,如果C、D满足|AC-BC|最大,而使|AD+BD|最小,则CD的长为
已知A(1,1),B(6,2),C、D分别为x轴、y轴上的动点,在运动的过程中,如果C、D满足|AC-BC|最大,而使|AD+BD|最小,则CD的长为