题目内容
18. 如图,在△ABC中,∠C=90°,分别以点A、B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧分别交于M、N两点,过M、N两点的直线交AC于点E,若AC=6,BC=3,则CE的长为( )
如图,在△ABC中,∠C=90°,分别以点A、B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧分别交于M、N两点,过M、N两点的直线交AC于点E,若AC=6,BC=3,则CE的长为( )| A. | $\frac{9}{4}$ | B. | $\frac{11}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{3}{2}$ |
分析 根据直角三角形两锐角互余可得∠A+∠CBA=90°,由作图可得MN是AB的垂直平分线,由线段垂直平分线的性质可得AE=EB,然后根据勾股定理即可得到结论.
解答 解:∵∠C=90°,
∴∠A+∠CBA=90°,
由作图可得MN是AB的垂直平分线,
∴AE=EB=6-CE,
∴CE2+BC2=BE2,
即CE2+32=(6-CE)2,
∴CE=$\frac{9}{4}$,
故选A.
点评 此题主要考查了线段垂直平分线的性质,以及三角形内角和定理,关键是掌握线段垂直平分线的作法.

练习册系列答案
相关题目
7.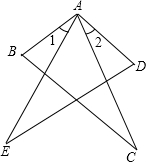 如图,要用“SAS”证△ABC≌△ADE,若已知AB=AD,AC=AE,则需要条件是( )
如图,要用“SAS”证△ABC≌△ADE,若已知AB=AD,AC=AE,则需要条件是( )
 如图,要用“SAS”证△ABC≌△ADE,若已知AB=AD,AC=AE,则需要条件是( )
如图,要用“SAS”证△ABC≌△ADE,若已知AB=AD,AC=AE,则需要条件是( )| A. | ∠1=∠2 | B. | ∠E=∠C | C. | ∠BAD=∠CAE | D. | ∠B=∠D |
 (1)如图,若图中小正方形的边长为1,则△ABC的面积为$\frac{7}{2}$.
(1)如图,若图中小正方形的边长为1,则△ABC的面积为$\frac{7}{2}$.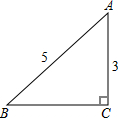 如图,在△ABC中,∠C=90°,则BC=4.
如图,在△ABC中,∠C=90°,则BC=4. 已知,如图,AB和DE是直立在地面上的两根立柱,AB=4m,某一时刻AB在阳光下的投影BC=3m,同一时刻测得DE影长为4.5m,则DE=6m.
已知,如图,AB和DE是直立在地面上的两根立柱,AB=4m,某一时刻AB在阳光下的投影BC=3m,同一时刻测得DE影长为4.5m,则DE=6m.