题目内容
15. 平行四边形ABCD中,BC=4,∠B=60°,AE为BC边上的高,将△ABE沿AE所在直线翻折后得△AFE,若△AFE与四边形AECD重叠部分的面积是$\frac{17\sqrt{3}}{4}$,则AB=8+3$\sqrt{2}$.
平行四边形ABCD中,BC=4,∠B=60°,AE为BC边上的高,将△ABE沿AE所在直线翻折后得△AFE,若△AFE与四边形AECD重叠部分的面积是$\frac{17\sqrt{3}}{4}$,则AB=8+3$\sqrt{2}$.
分析 根据题意可画出草图解题,由折叠特点可知△AFE≌△ABE,则∠F=∠B=60°,设CD与AF相交于点P,根据平行四边形的性质推出△CFP为等边三角形,△AFE与四边形AECD重叠部分的面积是△AEF与△CFP的面积之差,得出方程,解方程求出x,即可得出AB.
解答 解:根据沿直线折叠特点,△AFE≌△ABE,
∴∠F=∠B=60°,
在△ABE中,∠B=60°,设AB=2x,则AE=$\sqrt{3}$x,BE=x,
S△AFE=S△ABE=$\frac{1}{2}$x×$\sqrt{3}$x=$\frac{\sqrt{3}}{2}$x2,
CF=EF-EC=x-(BC-x)=2x-4,
∵在平行四边形ABCD中,CD∥AB,
∴∠PCF=∠B=60°=∠F,
∴△CFP为等边三角形,底边CF=2x-4,高为$\sqrt{3}$(x-2),
∴S△CFP=$\sqrt{3}$(x-2)2,
∴S重叠=S△AFE-S△CFP=$\frac{\sqrt{3}}{2}$x2-$\sqrt{3}$(x-2)2=$\frac{7\sqrt{3}}{4}$,
解得:x=$\frac{8+3\sqrt{2}}{2}$,或x=$\frac{8-3\sqrt{2}}{2}$,
∴AB=8$+3\sqrt{2}$,或AB=8-3$\sqrt{2}$(不合题意,舍去),
∴AB=8+3$\sqrt{2}$;
故答案为:8+3$\sqrt{2}$.
点评 本题考查了折叠的性质、平行四边形的性质、等边三角形的判定与性质等知识;熟练掌握折叠的性质,证明三角形是等边三角形是解决问题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
6.下列各式中是二次根式的是( )
| A. | $\sqrt{-7}$ | B. | $\root{4}{8}$ | C. | $\sqrt{{a}^{2}+1}$ | D. | $\root{3}{3}$ |
7.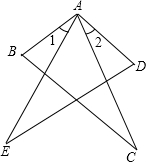 如图,要用“SAS”证△ABC≌△ADE,若已知AB=AD,AC=AE,则需要条件是( )
如图,要用“SAS”证△ABC≌△ADE,若已知AB=AD,AC=AE,则需要条件是( )
 如图,要用“SAS”证△ABC≌△ADE,若已知AB=AD,AC=AE,则需要条件是( )
如图,要用“SAS”证△ABC≌△ADE,若已知AB=AD,AC=AE,则需要条件是( )| A. | ∠1=∠2 | B. | ∠E=∠C | C. | ∠BAD=∠CAE | D. | ∠B=∠D |
5. 如图,在平面直角坐标系中,点A(2,2),分别以点O,A为圆心,大于$\frac{1}{2}$OA长为半径作弧,两弧交于点P.若点P的坐标为(m,n+1)(m≠1,n≠0),则n关于m的函数表达式为( )
如图,在平面直角坐标系中,点A(2,2),分别以点O,A为圆心,大于$\frac{1}{2}$OA长为半径作弧,两弧交于点P.若点P的坐标为(m,n+1)(m≠1,n≠0),则n关于m的函数表达式为( )
 如图,在平面直角坐标系中,点A(2,2),分别以点O,A为圆心,大于$\frac{1}{2}$OA长为半径作弧,两弧交于点P.若点P的坐标为(m,n+1)(m≠1,n≠0),则n关于m的函数表达式为( )
如图,在平面直角坐标系中,点A(2,2),分别以点O,A为圆心,大于$\frac{1}{2}$OA长为半径作弧,两弧交于点P.若点P的坐标为(m,n+1)(m≠1,n≠0),则n关于m的函数表达式为( )| A. | n=-m+1 | B. | n=-m+2 | C. | n=m+1 | D. | n=m+2 |
 若关于x的二次函数y=ax2+bx+c(a>0,c>1,a、b、c是常数)与x轴交于两个不同的点A(c,0),B(x0,0),与y轴交于点P,其图象顶点为点M,点O为坐标原点,且当0<x<c时,总有y>0.
若关于x的二次函数y=ax2+bx+c(a>0,c>1,a、b、c是常数)与x轴交于两个不同的点A(c,0),B(x0,0),与y轴交于点P,其图象顶点为点M,点O为坐标原点,且当0<x<c时,总有y>0.
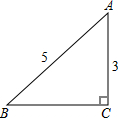 如图,在△ABC中,∠C=90°,则BC=4.
如图,在△ABC中,∠C=90°,则BC=4.