题目内容
19.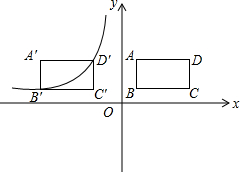 如图所示,在平面直角坐标系中,矩形ABCD,AB=2,BC=4,点B(1,1).
如图所示,在平面直角坐标系中,矩形ABCD,AB=2,BC=4,点B(1,1).(1)请直接写出点A,C,D的坐标:A(1,3),C(5,1),D(5,3);
(2)将矩形ABCD向左平移a个单位,得到矩形A′B′C′D′,使点B′,D′恰好同时落在反比例函数y=$\frac{k}{x}$(x<0)的图象上,求矩形ABCD平移的距离a及反比例函数的表达式.
分析 (1)根据B点的坐标和矩形的性质得出即可;
(2)根据题意得出B′和D′的坐标,代入函数解析式求出a的值,即可得出函数的解析式.
解答 解:(1)∵矩形ABCD,AB=2,BC=4,点B(1,1).
∴A(1,3),C(5,1),D(5,3),
故答案为:(1,3),(5,1),(5,3);
(2)根据题意得:B′(1-a,1),D′(5-a,3),
∵点B′,D′恰好同时落在反比例函数y=$\frac{k}{x}$(x<0)的图象上,
∴(1-a)×1=(5-a)×3,
解得:a=7,
∴B′(-6,1),
∴y=-$\frac{6}{x}$.
点评 本题考查了矩形的性质,用待定系数法求反比例函数的解析式,坐标与图形性质和平移等知识点,能求出B′的坐标是解此题的关键.

练习册系列答案
相关题目
10.若二次函数y=(m-1)x2+2x+1的图象与x轴有两个不同的交点,则m的取值范围是( )
| A. | m≤2 | B. | m<2 | C. | m≤2且m≠1 | D. | m<2且m≠1 |
14. 已知:正方体展开图(如图所示)相对面上的数值相等,那么x的值等于( )
已知:正方体展开图(如图所示)相对面上的数值相等,那么x的值等于( )
 已知:正方体展开图(如图所示)相对面上的数值相等,那么x的值等于( )
已知:正方体展开图(如图所示)相对面上的数值相等,那么x的值等于( )| A. | -1 | B. | a-2 | C. | -1或2 | D. | 1或-2 |
11.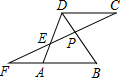 如图,点P是菱形ABCD对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F,则线段PC、PE、PF之间存在的数量关系是( )
如图,点P是菱形ABCD对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F,则线段PC、PE、PF之间存在的数量关系是( )
 如图,点P是菱形ABCD对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F,则线段PC、PE、PF之间存在的数量关系是( )
如图,点P是菱形ABCD对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F,则线段PC、PE、PF之间存在的数量关系是( )| A. | 2PC=PE+PF | B. | 2PC=PE•PF | C. | PC2=PE•PF | D. | PC2=$\frac{PF}{PE}$ |
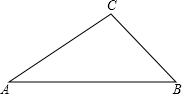
 如图,求证:∠BDC=∠A+∠B+∠C.
如图,求证:∠BDC=∠A+∠B+∠C.
 已知:如图,在△ABC中,∠ABC=45°,tanA=$\frac{3}{4}$,AB=14,
已知:如图,在△ABC中,∠ABC=45°,tanA=$\frac{3}{4}$,AB=14,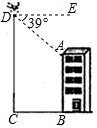 如图,某校无人机兴趣小组借助无人机测量教学楼的高度AB,无人机在离教学楼底部B处16米的C处垂直上升31米至D处,测得教学楼顶A处的俯角为39°,求教学楼的高度AB.(结果精确到0.1米)【参考数据:sin39°=0.63,cos39°=0.78,tan39°=0.81】
如图,某校无人机兴趣小组借助无人机测量教学楼的高度AB,无人机在离教学楼底部B处16米的C处垂直上升31米至D处,测得教学楼顶A处的俯角为39°,求教学楼的高度AB.(结果精确到0.1米)【参考数据:sin39°=0.63,cos39°=0.78,tan39°=0.81】