题目内容
16. 如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PD=2,求PC的长.
如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PD=2,求PC的长.
分析 作PE⊥OA于E,根据角平分线的性质求出PE,根据直角三角形的性质和平行线的性质解答即可.
解答  解:作PE⊥OA于E,
解:作PE⊥OA于E,
∵OP平分∠AOB,PD⊥OB,PE⊥OA,
∴PE=PD=2,
∵OP平分∠AOB,∠AOP=15°,
∴∠AOB=30°,
∵PC∥OB,
∴∠ECP=∠AOB=30°,
∴PC=2PE=4.
点评 本题考查的是角平分线的性质、直角三角形的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
11.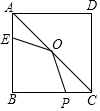 如图,在正方形ABCD中,边长为4,E为AB上的点,且AE=1,O为AC的中点,P为BC上的动点,则△EOP周长的最小值是( )
如图,在正方形ABCD中,边长为4,E为AB上的点,且AE=1,O为AC的中点,P为BC上的动点,则△EOP周长的最小值是( )
 如图,在正方形ABCD中,边长为4,E为AB上的点,且AE=1,O为AC的中点,P为BC上的动点,则△EOP周长的最小值是( )
如图,在正方形ABCD中,边长为4,E为AB上的点,且AE=1,O为AC的中点,P为BC上的动点,则△EOP周长的最小值是( )| A. | 4+3$\sqrt{2}$ | B. | $\sqrt{29}$+$\sqrt{5}$ | C. | 2+$\sqrt{5}$+3$\sqrt{2}$ | D. | $\sqrt{5}$+$\sqrt{2}$ |
1.下列各式中,正确的是( )
| A. | $\sqrt{36}$=±6 | B. | $\root{3}{-8}$=-$\root{3}{8}$ | C. | $\sqrt{(-4)^{2}}$=-4 | D. | -$\sqrt{3.6}$=-0.6 |
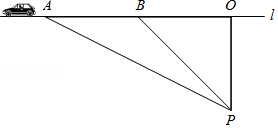 交通安全是社会关注的热点问题,安全隐患主要是超速和超载.某中学八年级数学活动小组的同学进行了测试汽车速度的实验.如图,先在笔直的公路1旁选取一点P,在公路1上确定点O、B,使得PO⊥l,PO=100米,∠PBO=45°.这时,一辆轿车在公路1上由B向A匀速驶来,测得此车从B处行驶到A处所用的时间为3秒,并测得∠APO=60°.此路段限速每小时80千米,试判断此车是否超速?请说明理由(参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73).
交通安全是社会关注的热点问题,安全隐患主要是超速和超载.某中学八年级数学活动小组的同学进行了测试汽车速度的实验.如图,先在笔直的公路1旁选取一点P,在公路1上确定点O、B,使得PO⊥l,PO=100米,∠PBO=45°.这时,一辆轿车在公路1上由B向A匀速驶来,测得此车从B处行驶到A处所用的时间为3秒,并测得∠APO=60°.此路段限速每小时80千米,试判断此车是否超速?请说明理由(参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73).