题目内容
12. 如图,已知AB为⊙O的直径,点E在⊙O上,∠EAB的平分线交⊙O于点C,过点C作AE的垂线,垂足为D,直线DC与AB的延长线交于点P.
如图,已知AB为⊙O的直径,点E在⊙O上,∠EAB的平分线交⊙O于点C,过点C作AE的垂线,垂足为D,直线DC与AB的延长线交于点P.(1)判断直线PC与⊙O的位置关系,并说明理由;
(2)若tan∠P=$\frac{3}{4}$,AD=6,求线段AE的长.
分析 (1)结论:PC是⊙O的切线.只要证明OC∥AD,推出∠OCP=∠D=90°,即可.
(2)由OC∥AD,推出$\frac{OC}{AD}$=$\frac{OP}{AP}$,即$\frac{r}{6}$=$\frac{10-r}{10}$,解得r=$\frac{15}{4}$,由BE∥PD,AE=AB•sin∠ABE=AB•sin∠P,由此即可计算.
解答 解:(1)结论:PC是⊙O的切线.
理由:连接OC.
∵AC平分∠EAB,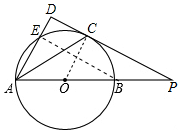
∴∠EAC=∠CAB,
又∵∠CAB=∠ACO,
∴∠EAC=∠OCA,
∴OC∥AD,
∵AD⊥PD,
∴∠OCP=∠D=90°,
∴PC是⊙O的切线.
(2)连接BE.在Rt△ADP中,∠ADP=90°,AD=6,tan∠P=$\frac{3}{4}$,
∴PD=8,AP=10,设半径为r,
∵OC∥AD,
∴$\frac{OC}{AD}$=$\frac{OP}{AP}$,即$\frac{r}{6}$=$\frac{10-r}{10}$,
解得r=$\frac{15}{4}$,
∵AB是直径,
∴∠AEB=∠D=90°,
∴BE∥PD,
∴AE=AB•sin∠ABE=AB•sin∠P=$\frac{15}{4}$×$\frac{3}{5}$=$\frac{9}{2}$.
点评 本题考查直线与圆的位置关系、切线的判定、解直角三角形、平行线的性质、锐角三角函数等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3. 如图,A,B是数轴上两点,过点B作BC⊥x轴,若BC=2,以A为圆心,AC为半径作圆弧交数轴于点P,若点P所表示的数是$\sqrt{13}$-2,则点A表示的数是( )
如图,A,B是数轴上两点,过点B作BC⊥x轴,若BC=2,以A为圆心,AC为半径作圆弧交数轴于点P,若点P所表示的数是$\sqrt{13}$-2,则点A表示的数是( )
 如图,A,B是数轴上两点,过点B作BC⊥x轴,若BC=2,以A为圆心,AC为半径作圆弧交数轴于点P,若点P所表示的数是$\sqrt{13}$-2,则点A表示的数是( )
如图,A,B是数轴上两点,过点B作BC⊥x轴,若BC=2,以A为圆心,AC为半径作圆弧交数轴于点P,若点P所表示的数是$\sqrt{13}$-2,则点A表示的数是( )| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
20.如果将“收入100元”记作“+100元”,那么“支出50元”应记作( )
| A. | +50元 | B. | -50元 | C. | +150元 | D. | -150元 |
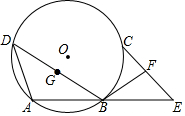 如图,点A、B、C、D在⊙O上,且$\widehat{AD}$=$\widehat{BC}$,E是AB延长线上一点,且BE=AB,F是EC的中点.
如图,点A、B、C、D在⊙O上,且$\widehat{AD}$=$\widehat{BC}$,E是AB延长线上一点,且BE=AB,F是EC的中点.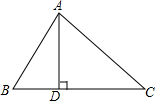 如图,在△ABC中,AD是BC边上的高,∠B=45°,∠C=60°,AD=2,求BC的长.(结果保留根号)
如图,在△ABC中,AD是BC边上的高,∠B=45°,∠C=60°,AD=2,求BC的长.(结果保留根号) 在一次课外实践活动中,同学们要测量某公园人工湖两侧A、B两个凉亭之间的距离.现测得AC=300m,BC=700m,∠CAB=120°,请计算A、B两个凉亭之间的距离.
在一次课外实践活动中,同学们要测量某公园人工湖两侧A、B两个凉亭之间的距离.现测得AC=300m,BC=700m,∠CAB=120°,请计算A、B两个凉亭之间的距离. 如图四边形ABCD中,∠C=90°,BC=1,DC=2,AB=$\sqrt{14}$,AD=3,求出这个四边形的面积.
如图四边形ABCD中,∠C=90°,BC=1,DC=2,AB=$\sqrt{14}$,AD=3,求出这个四边形的面积.