题目内容
4.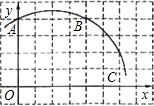 如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.
如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.(1)用直尺画出该圆弧所在圆的圆心M的位置并写出点M的坐标;
(2)若A点的坐标为(0,4),D点的坐标为(7,0),求证直线CD是⊙M的切线.
分析 (1)作AB和BC的垂直平分线,两线交于一点M,点M即为所求,由图形可知:这点的坐标是(2,0);
(2)设过C点与x轴垂直的直线与x轴的交点为E,连结MC,作直线CD.得出CE=2,ME=4,ED=1,MD=5,根据勾股定理求出MC2=20,CD2=5,推出∠MCD=90°,根据切线的判定推出即可.
解答 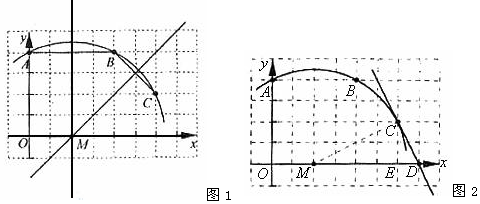 解:(1)如图1,连接AB、BC,
解:(1)如图1,连接AB、BC,
作AB和BC的垂直平分线,两线交于一点M,点M即为所求,
由图形可知:这点的坐标是(2,0),
∴圆弧所在圆的圆心M点的坐标是(2,0);
(2)由A(0,4),可得小正方形的边长为1,从而可得B(4,4)、C(6,2),
如图2,设过C点与x轴垂直的直线与x轴的交点为E,连结MC,作直线CD.
∴CE=2,ME=4,ED=1,MD=5,
在Rt△CEM中,∠CEM=90°,
∴MC2=ME2+CE2=42+22=20,
在Rt△CED中,∠CED=90°,
∴CD2=ED2+CE2=12+22=5,
∴MD2=MC2+CD2,
∴∠MCE=90°,
∵MC为半径,
∴直线CD是⊙M的切线.
点评 本题考查了勾股定理,切线的判定等,在判定一条直线为圆的切线时,当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径;当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.

练习册系列答案
相关题目
12.如表是二次函数y=ax2+bx+c(a≠0)的自变量x与函数值y的对应关系,一元二次方程ax2+bx+c=$\frac{3}{10}$(a≠0)的一个解x的取值范围是6.2<x<6.3.
| x | 6.1 | 6.2 | 6.3 | 6.4 |
| y=ax2+bx+c | -0.3 | -0.1 | 0.2 | 0.4 |
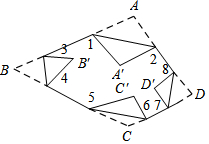 如图所示,把一个四边形纸片ABCD的四个顶角分别向内折叠,折叠之后,4个顶点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8的度数是720°.
如图所示,把一个四边形纸片ABCD的四个顶角分别向内折叠,折叠之后,4个顶点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8的度数是720°.
 在如图所示的平面直角坐标系中表示下面各点:A(0,3),B(1,-3),C(3,-5),D(-3,-5),E(3,5),F(5,7),G(5,0).
在如图所示的平面直角坐标系中表示下面各点:A(0,3),B(1,-3),C(3,-5),D(-3,-5),E(3,5),F(5,7),G(5,0).