题目内容
19.x、y均为实数y<$\sqrt{x-1}$+$\sqrt{1-x}$+$\frac{1}{2}$,化简:$\frac{\sqrt{(1-y)^{2}}}{y-1}$.分析 根据被开方数大于等于0列不等式求出x的值,从而得到y的取值范围,再根据二次根式的性质化简即可.
解答 解:由题意得,x-1≥0且1-x≥0,
解得x≥1且x≤1,
所以,x=1,
y<$\frac{1}{2}$,
所以,$\frac{\sqrt{(1-y)^{2}}}{y-1}$=$\frac{1-y}{y-1}$=-1.
点评 本题考查了二次根式有意义的条件,二次根式中的被开方数必须是非负数,否则二次根式无意义.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
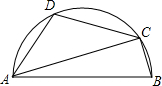 如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=20°,$\widehat{AD}$=$\widehat{CD}$,求:∠BCD的度数.
如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=20°,$\widehat{AD}$=$\widehat{CD}$,求:∠BCD的度数. 如图,∠ABC可以表示成∠1或∠B,∠α可以表示成∠ACB,∠2可以表示成∠CAD.
如图,∠ABC可以表示成∠1或∠B,∠α可以表示成∠ACB,∠2可以表示成∠CAD.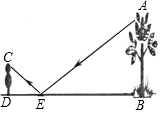 如图,王华把一面很小的镜子水平放置在离树底(点B)8米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢(点A),已知DE=4米,王华目高CD=1.6米,则树的高度AB为( )
如图,王华把一面很小的镜子水平放置在离树底(点B)8米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢(点A),已知DE=4米,王华目高CD=1.6米,则树的高度AB为( )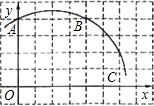 如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.
如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.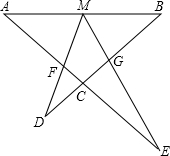 如图,AE与BD交于点C,∠DME=∠A=∠B,且DM交AC于F,ME交BC于G
如图,AE与BD交于点C,∠DME=∠A=∠B,且DM交AC于F,ME交BC于G