题目内容
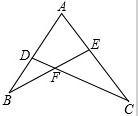 如图所示,已知AD•AB=AE•AC,求证:△ABE∽△ACD.
如图所示,已知AD•AB=AE•AC,求证:△ABE∽△ACD.考点:相似三角形的判定
专题:证明题
分析:由AD•AB=AE•AC可得到
=
,结合公共角可证得结论.
| AD |
| AC |
| AE |
| AB |
解答:证明:∵AD•AB=AE•AC,
∴
=
,且∠DAE=∠CAB,
∴△ABE∽△ACD.
∴
| AD |
| AC |
| AE |
| AB |
∴△ABE∽△ACD.
点评:本题主要考查相似三角形的判定,掌握相似三角形的判定方法是解题的关键,即利用两边对应成比例且夹角相等可证明两三角形相似.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
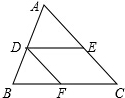 如图,在△ABC中,点D、E、F分别在AB、AC、BC上,DE∥BC,DF∥AC,下列比例式中,正确的是( )
如图,在△ABC中,点D、E、F分别在AB、AC、BC上,DE∥BC,DF∥AC,下列比例式中,正确的是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列说法正确的是( )
A、在Rt△ABC中,sinA=
| ||
B、在△ABC中,sinA=
| ||
| C、在Rt△ABC中,0<sinA≤1 | ||
| D、在Rt△ABC中,sinA=sinB |
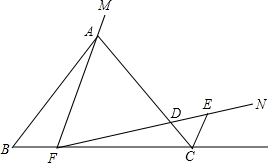 如图,△ABC是等边三角形,点F在直线BC上,∠MFN=60°,∠MFN的一边FM始终过△ABC的顶点A,另一边FN与△ABC的外角平分线交于点E,当点F在BC的任意位置时,写出关于线段FA、FE的数量关系的猜想,并证明你的猜想.
如图,△ABC是等边三角形,点F在直线BC上,∠MFN=60°,∠MFN的一边FM始终过△ABC的顶点A,另一边FN与△ABC的外角平分线交于点E,当点F在BC的任意位置时,写出关于线段FA、FE的数量关系的猜想,并证明你的猜想. 已知AD⊥BD,BC⊥CD,AB=a cm,BC=b cm,则BD的取值范围是
已知AD⊥BD,BC⊥CD,AB=a cm,BC=b cm,则BD的取值范围是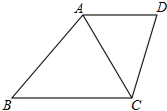 如图,在梯形ABCD中,AD∥BC,∠B=∠ACD,若AC=12,BC=16.
如图,在梯形ABCD中,AD∥BC,∠B=∠ACD,若AC=12,BC=16. 如图,直线l的解析式为y=
如图,直线l的解析式为y=