题目内容
下列说法正确的是( )
A、在Rt△ABC中,sinA=
| ||
B、在△ABC中,sinA=
| ||
| C、在Rt△ABC中,0<sinA≤1 | ||
| D、在Rt△ABC中,sinA=sinB |
考点:解直角三角形
专题:
分析:在直角三角形中根据三角函数的定义逐项判断即可.
解答:解:
A、正弦函数值是线段的比,所以由sinA=
并不一定有a=1,c=2,所以A不正确;
B、因为只有在直角三角形中sinA=
=
,才可设a=k,c=2k,所以B不正确;
C、在Rt△ABC中,最大角为90°,所以sinA最大值为1,所以C正确;
D、只有当∠A=∠B=45°时,才有sinA=sinB,所以D不正确;
故选C.
A、正弦函数值是线段的比,所以由sinA=
| 1 |
| 2 |
B、因为只有在直角三角形中sinA=
| a |
| c |
| 1 |
| 2 |
C、在Rt△ABC中,最大角为90°,所以sinA最大值为1,所以C正确;
D、只有当∠A=∠B=45°时,才有sinA=sinB,所以D不正确;
故选C.
点评:本题主要考查三角函数的定义,掌握三角函数的定义是解题的关键,即在直角三角形中∠A为锐角,则sinA=
,cosA=
,tanA=
.
| a |
| c |
| b |
| c |
| a |
| b |

练习册系列答案
相关题目
在Rt△ABC中,∠C=90°,AC=6,BC=8,则sinB的值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
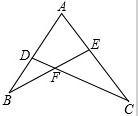 如图所示,已知AD•AB=AE•AC,求证:△ABE∽△ACD.
如图所示,已知AD•AB=AE•AC,求证:△ABE∽△ACD.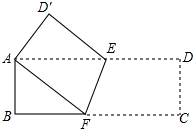 如图,ABCD是一张长方形纸片,AB=CD=3,BC=AD=9.在边AD上取一点E,在BC上取一点F,将纸片沿EF折叠,点C恰好落在点A处,则线段EF的长度为
如图,ABCD是一张长方形纸片,AB=CD=3,BC=AD=9.在边AD上取一点E,在BC上取一点F,将纸片沿EF折叠,点C恰好落在点A处,则线段EF的长度为


