题目内容
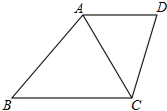 如图,在梯形ABCD中,AD∥BC,∠B=∠ACD,若AC=12,BC=16.
如图,在梯形ABCD中,AD∥BC,∠B=∠ACD,若AC=12,BC=16.(1)试说明△ABC和△ACD相似;
(2)试求梯形ABCD的中位线的长度.
考点:相似三角形的判定,梯形中位线定理
专题:
分析:(1)由平行可得∠ACB=∠DAC,结合条件可证明△ABC∽△CDA;
(2)利用(1)可求得
=
,可求得AD,再利用梯形中位线定理求得中位线的长度.
(2)利用(1)可求得
| BC |
| AC |
| AC |
| AD |
解答:解:(1)∵AD∥BC,
∴∠ACB=∠DAC,且∠B=∠ACD,
∴△ABC∽△CDA;
(2)由△ABC∽△CDA可得
=
,
∴
=
,
解得AD=9,
∴梯形ABCD的中位线=
(AD+BC)=
×(9+16)=12.5.
∴∠ACB=∠DAC,且∠B=∠ACD,
∴△ABC∽△CDA;
(2)由△ABC∽△CDA可得
| BC |
| AC |
| AC |
| AD |
∴
| 16 |
| 12 |
| 12 |
| AD |
解得AD=9,
∴梯形ABCD的中位线=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查相似三角形的判定和性质,注意利用平行可寻找角相等,从而可以找到三角形相似的条件,在求中位线时求得AD是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
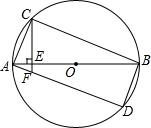 如图,矩形ABCD,AB是⊙O的直径,CE⊥AB,垂足为E,交AD于F,求证:AC2=AF•AD.
如图,矩形ABCD,AB是⊙O的直径,CE⊥AB,垂足为E,交AD于F,求证:AC2=AF•AD.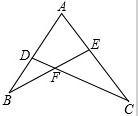 如图所示,已知AD•AB=AE•AC,求证:△ABE∽△ACD.
如图所示,已知AD•AB=AE•AC,求证:△ABE∽△ACD.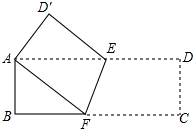 如图,ABCD是一张长方形纸片,AB=CD=3,BC=AD=9.在边AD上取一点E,在BC上取一点F,将纸片沿EF折叠,点C恰好落在点A处,则线段EF的长度为
如图,ABCD是一张长方形纸片,AB=CD=3,BC=AD=9.在边AD上取一点E,在BC上取一点F,将纸片沿EF折叠,点C恰好落在点A处,则线段EF的长度为