题目内容
已知方程x2+(k+1)x+k=0的两根平方和是5,求k的值.
考点:根与系数的关系
专题:
分析:设方程两根分别为a、b,根据根与系数的关系得到a+b=-(k+1),ab=k,再利用完全平方公式把a2+b2=5变形得到(a+b)2-2ab=5,则(k+1)2-2•k=5,求出k的值,再利用判别式确定满足条件的k的值.
解答:解:设方程两根分别为a、b,根据题意得:
a+b=-(k+1),ab=k,
∵a2+b2=5,
∴(a+b)2-2ab=5,
∴(k+1)2-2•k=5,
整理得k2=4,
解得k1=-2,k2=2,
当k=-2时,原方程变形为x2-x-2=0,△>0,方程有两个不相等的实数解;
当k=2时,原方程变形为x2+3x+2=0,△>0,方程有两个不相等的实数解;
∴k的值为±2.
a+b=-(k+1),ab=k,
∵a2+b2=5,
∴(a+b)2-2ab=5,
∴(k+1)2-2•k=5,
整理得k2=4,
解得k1=-2,k2=2,
当k=-2时,原方程变形为x2-x-2=0,△>0,方程有两个不相等的实数解;
当k=2时,原方程变形为x2+3x+2=0,△>0,方程有两个不相等的实数解;
∴k的值为±2.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
在Rt△ABC中,∠C=90°,AC=6,BC=8,则sinB的值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列各式成立的是( )
A、
| ||||||
B、-(
| ||||||
C、
| ||||||
D、
|
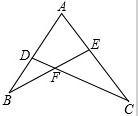 如图所示,已知AD•AB=AE•AC,求证:△ABE∽△ACD.
如图所示,已知AD•AB=AE•AC,求证:△ABE∽△ACD.


