题目内容
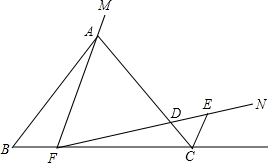 如图,△ABC是等边三角形,点F在直线BC上,∠MFN=60°,∠MFN的一边FM始终过△ABC的顶点A,另一边FN与△ABC的外角平分线交于点E,当点F在BC的任意位置时,写出关于线段FA、FE的数量关系的猜想,并证明你的猜想.
如图,△ABC是等边三角形,点F在直线BC上,∠MFN=60°,∠MFN的一边FM始终过△ABC的顶点A,另一边FN与△ABC的外角平分线交于点E,当点F在BC的任意位置时,写出关于线段FA、FE的数量关系的猜想,并证明你的猜想.考点:全等三角形的判定与性质
专题:
分析:作FG∥AC,易证AG=FC和∠AGF=120°、∠BCE=120°、∠CFE=∠BAF,即可证明△AGF≌△FCE,即可求得AF=EF.
解答:证明:作FG∥AC,

∵FG∥AC,
∴△BGF是等边三角形,
∴BG=BF,∠AGF=120°,
∴AG=FC,
∵CE平分∠ACB外角,
∴∠BCE=120°,
∵∠AFC=∠B+∠BAF=∠AFD+∠CFE,∠MFE=60°,
∴∠CFE=∠BAF,
∵在△AGF和△FCE中,
,
∴△AGF≌△FCE,(ASA)
∴AF=EF.

∵FG∥AC,
∴△BGF是等边三角形,
∴BG=BF,∠AGF=120°,
∴AG=FC,
∵CE平分∠ACB外角,
∴∠BCE=120°,
∵∠AFC=∠B+∠BAF=∠AFD+∠CFE,∠MFE=60°,
∴∠CFE=∠BAF,
∵在△AGF和△FCE中,
|
∴△AGF≌△FCE,(ASA)
∴AF=EF.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△AGF≌△FCE是解题的关键.

练习册系列答案
相关题目
在Rt△ABC中,∠C=90°,AC=6,BC=8,则sinB的值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,把长方形纸片ABCD沿EF折叠,∠1=50°,则∠BFE=
如图,把长方形纸片ABCD沿EF折叠,∠1=50°,则∠BFE=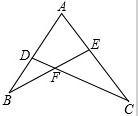 如图所示,已知AD•AB=AE•AC,求证:△ABE∽△ACD.
如图所示,已知AD•AB=AE•AC,求证:△ABE∽△ACD.