题目内容
5. 如图,AB是半圆O的直径,过点O作弦AD的垂线交半圆O于点E,交AC于点C,使∠BED=∠C.
如图,AB是半圆O的直径,过点O作弦AD的垂线交半圆O于点E,交AC于点C,使∠BED=∠C.(1)判断直线AC与⊙O的位置关系,并证明你的结论;
(2)若AC=8,cos∠BED=$\frac{4}{5}$,求AD的长.
分析 (1)根据OC⊥AD,可得∠AOC+∠2=90°,然后根据∠BED=∠C,证明∠AOC+∠C=90°,据此即可证得C是圆O的切线;
(2)在直角△AOC中利用三角函数和勾股定理求得OC和OA的长度,然后利用三角形的面积公式求得AF的长,再根据垂径定理求解.
解答 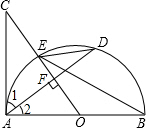 解:(1)AC与圆O相切.证明如下:
解:(1)AC与圆O相切.证明如下:
∵OC⊥AD,
∴∠AOC+∠2=90°
∵∠C=∠BED=∠2,
∴∠AOC+∠C=90°,即∠CAO=90°,
∴AC与⊙O相切;
(2)∵∠BED=∠C,
∴直角△AOC中,cosC=$\frac{AC}{OC}$=os∠BED=$\frac{4}{5}$,
∴OC=$\frac{AC}{cos∠C}$=$\frac{8}{\frac{4}{5}}$=10,
∴AO=$\sqrt{O{C}^{2}-A{C}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
又∵S△AOC=$\frac{1}{2}$AC•OA=$\frac{1}{2}$OC•AF,
∴AF=$\frac{AC•OA}{OC}$=$\frac{8×6}{10}$=$\frac{24}{5}$.
∵OC⊥AD,
∴AC=2AF=$\frac{48}{5}$.
点评 本题考查了切线的判定以及垂径定理,利用三角形的面积公式求得AF的长是关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
16.在平面直角坐标系中,点(a-3,2a+1)在第二象限内,则a的取值范围是( )
| A. | -3<a<$\frac{1}{2}$ | B. | $\frac{1}{2}$<a<3 | C. | -3<a<-$\frac{1}{2}$ | D. | $-\frac{1}{2}$<a<3 |
13. 数学课上探究一次函数图象与反比例函数图象有交点时的相关结论:已知直线y=kx+b与x轴、y轴分别交于点C(x,0)、D(0,y),与双曲线y=$\frac{m}{x}$交于点A(x1,y1),B(x2,y2).
数学课上探究一次函数图象与反比例函数图象有交点时的相关结论:已知直线y=kx+b与x轴、y轴分别交于点C(x,0)、D(0,y),与双曲线y=$\frac{m}{x}$交于点A(x1,y1),B(x2,y2).
(1)填空与观察:
(2)发现与验证:
数学学习小组在探究图象交点时发现以下结论:
①x1+x2=x;②y1+y2=y;③当b2+4mk≥0时,两函数图象一定会相交.
你认为以上探究的结论中正确的有①②③(填序号),请选择一个加以证明.
(3)应用与拓展:
连接AO,BO,判断△ACO与△BOD的面积有什么关系,并说明理由.
 数学课上探究一次函数图象与反比例函数图象有交点时的相关结论:已知直线y=kx+b与x轴、y轴分别交于点C(x,0)、D(0,y),与双曲线y=$\frac{m}{x}$交于点A(x1,y1),B(x2,y2).
数学课上探究一次函数图象与反比例函数图象有交点时的相关结论:已知直线y=kx+b与x轴、y轴分别交于点C(x,0)、D(0,y),与双曲线y=$\frac{m}{x}$交于点A(x1,y1),B(x2,y2).(1)填空与观察:
| 函数关系式 | C(x,0) | D(0,y) | A (x1,y1) | B(x2,y2) |
| y=2x+2,y=$\frac{4}{x}$,如图1 | (-1,0) | (0,2) | (1 , 4) | (-2,-2) |
| y=x-3,y=$\frac{10}{x}$,如图2 | (3,0) | (0,-3) | (5,2) | ( -2, -5) |
数学学习小组在探究图象交点时发现以下结论:
①x1+x2=x;②y1+y2=y;③当b2+4mk≥0时,两函数图象一定会相交.
你认为以上探究的结论中正确的有①②③(填序号),请选择一个加以证明.
(3)应用与拓展:
连接AO,BO,判断△ACO与△BOD的面积有什么关系,并说明理由.
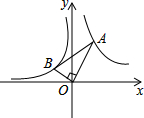 如图,已知第一象限内的点A在反比例函数y=$\frac{2}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,tanA=$\frac{1}{3}$,则k的值为-$\frac{2}{9}$.
如图,已知第一象限内的点A在反比例函数y=$\frac{2}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,tanA=$\frac{1}{3}$,则k的值为-$\frac{2}{9}$.
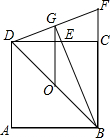 如图,O是正方形ABCD的中心,BE平分∠DBC,交DC于点E,将点E绕着点C按顺时针方向旋转90°得到点F,连接CF,DF,BE的延长线交DF于点G,连接OG.
如图,O是正方形ABCD的中心,BE平分∠DBC,交DC于点E,将点E绕着点C按顺时针方向旋转90°得到点F,连接CF,DF,BE的延长线交DF于点G,连接OG.