题目内容
8.在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE.(1)如图1,当∠ABC=45°时,求证:AD=DE;
(2)如图2,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由.
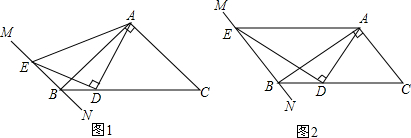
分析 (1)首先过点D作DF⊥BC,交AB于点F,得出∠BDE=∠ADF,以及∠EBD=∠AFD,再得出△BDE≌△FDA(ASA),求出即可;
(2)首先过点D作DG⊥BC,交AB于点G,进而得出∠EBD=∠AGD,证出△BDE∽△GDA即可得出答案.
解答  (1)证明:如图1,过点D作DF⊥BC,交AB于点F,
(1)证明:如图1,过点D作DF⊥BC,交AB于点F,
则∠BDE+∠FDE=90°,
∵DE⊥AD,
∴∠FDE+∠ADF=90°,
∴∠BDE=∠ADF,
∵∠BAC=90°,∠ABC=45°,
∴∠C=45°,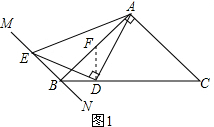
∵MN∥AC,
∴∠EBD=180°-∠C=135°,
∵∠BFD=45°,DF⊥BC,
∴∠BFD=45°,BD=DF,
∴∠AFD=135°,
∴∠EBD=∠AFD,
在△BDE和△FDA中
$\left\{\begin{array}{l}{∠EBD=∠AFD}\\{BD=DF}\\{∠BDE=∠ADF}\end{array}\right.$,
∴△BDE≌△FDA(ASA),
∴AD=DE;
(2)解:DE=$\sqrt{3}$AD,
理由:如图2,过点D作DG⊥BC,交AB于点G,
则∠BDE+∠GDE=90°,
∵DE⊥AD,
∴∠GDE+∠ADG=90°,
∴∠BDE=∠ADG,
∵∠BAC=90°,∠ABC=30°,
∴∠C=60°,
∵MN∥AC,
∴∠EBD=180°-∠C=120°,
∵∠ABC=30°,DG⊥BC,
∴∠BGD=60°,
∴∠AGD=120°,
∴∠EBD=∠AGD,
∴△BDE∽△GDA,
∴$\frac{AD}{DE}$=$\frac{DG}{BD}$,
在Rt△BDG中,$\frac{DG}{BD}$=tan30°=$\frac{\sqrt{3}}{3}$,
∴DE=$\sqrt{3}$AD.
点评 此题主要考查了全等三角形的判定与性质以及相似三角形的判定与性质,得出△EBD∽△AGD是解题关键.

 如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为( )
如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为( )| A. | 130° | B. | 100° | C. | 65° | D. | 50° |
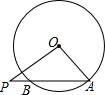 如图,已知⊙O的半径为6,弦AB的长为8,P是AB延长线上一点,BP=2,则tan∠OPA的值是$\frac{{\sqrt{5}}}{3}$.
如图,已知⊙O的半径为6,弦AB的长为8,P是AB延长线上一点,BP=2,则tan∠OPA的值是$\frac{{\sqrt{5}}}{3}$. 如图,方格图中每个小正方形的边长为1,点A、B、C都是格点.
如图,方格图中每个小正方形的边长为1,点A、B、C都是格点.
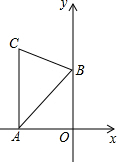 如图,AC⊥x轴于点A,点B在y轴的正半轴上,∠ABC=60°,AB=4,BC=2$\sqrt{3}$,点D为AC与反比例函数y=$\frac{k}{x}$的图象的交点.若直线BD将△ABC的面积分成1:2的两部分,则k的值为-4或-8.
如图,AC⊥x轴于点A,点B在y轴的正半轴上,∠ABC=60°,AB=4,BC=2$\sqrt{3}$,点D为AC与反比例函数y=$\frac{k}{x}$的图象的交点.若直线BD将△ABC的面积分成1:2的两部分,则k的值为-4或-8.