题目内容
18.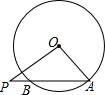 如图,已知⊙O的半径为6,弦AB的长为8,P是AB延长线上一点,BP=2,则tan∠OPA的值是$\frac{{\sqrt{5}}}{3}$.
如图,已知⊙O的半径为6,弦AB的长为8,P是AB延长线上一点,BP=2,则tan∠OPA的值是$\frac{{\sqrt{5}}}{3}$.
分析 作OM⊥AB于M,由垂径定理得出AM=BM=$\frac{1}{2}$AB=4cm,由勾股定理求出OM,再由三角函数的定义即可得出结果.
解答 解:作OM⊥AB于M,如图所示:
则AM=BM=$\frac{1}{2}$AB=4cm,
∴OM=$\sqrt{O{A}^{2}-A{M}^{2}}$=2$\sqrt{5}$,
∵PM=PB+BM=6,
∴tan∠OPA=$\frac{OM}{PM}$=$\frac{2\sqrt{5}}{6}$=$\frac{\sqrt{5}}{3}$;
故答案为:$\frac{\sqrt{5}}{3}$.
点评 本题考查了垂径定理、解直角三角形、勾股定理、三角函数的定义;熟练掌握垂径定理,由勾股定理求出OM是解决问题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
6.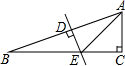 如图,在△ABC中,∠C=90°,∠B=22.5°,AB的垂直平分线交AB于D,交BC于E,若CE=1,则BE的长是( )
如图,在△ABC中,∠C=90°,∠B=22.5°,AB的垂直平分线交AB于D,交BC于E,若CE=1,则BE的长是( )
 如图,在△ABC中,∠C=90°,∠B=22.5°,AB的垂直平分线交AB于D,交BC于E,若CE=1,则BE的长是( )
如图,在△ABC中,∠C=90°,∠B=22.5°,AB的垂直平分线交AB于D,交BC于E,若CE=1,则BE的长是( )| A. | 3 | B. | $\sqrt{2}$ | C. | 2 | D. | 6 |
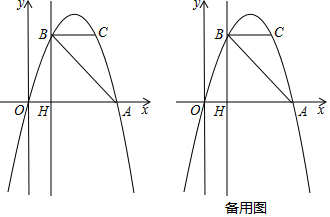
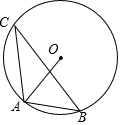 如图,A、B、C是⊙O上三点,∠OAB=56°,则∠ACB的度数是34°.
如图,A、B、C是⊙O上三点,∠OAB=56°,则∠ACB的度数是34°. 国家推行“节能减排,低碳经济”政策后,某环保节能设备生产的产品供不应求,若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于44万元,每套产品的售价不低于80万元.已知这种设备的月产量x(套)与每套的售价y1(万元)间满足关系式y1=160-2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.
国家推行“节能减排,低碳经济”政策后,某环保节能设备生产的产品供不应求,若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于44万元,每套产品的售价不低于80万元.已知这种设备的月产量x(套)与每套的售价y1(万元)间满足关系式y1=160-2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.