题目内容
16.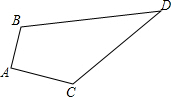 如图,四边形ABCD中,AB=3cm,AC=4cm,BD=13cm,CD=12cm,且∠A=90°,求△BCD的面积.
如图,四边形ABCD中,AB=3cm,AC=4cm,BD=13cm,CD=12cm,且∠A=90°,求△BCD的面积.
分析 连接BC,先根据勾股定理求出BC的长,再由勾股定理的逆定理判断出△BCD的形状,由三角形的面积公式即可得出结论.
解答 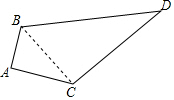 解:连接BC,
解:连接BC,
∵∠A=90°,
∴△ABC为直角三角形,
∵AC=4cm,AB=3cm,
∴根据勾股定理得:BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=5cm,
在△BCD中,BC2+CD2=52+122=25+144=169,DD2=132=169,
∵BC2+CD2=BD2,
∴△BCD为直角三角形,
∴S△BCD=$\frac{1}{2}$BC•CD=$\frac{1}{2}$×5×12=30(cm2)
点评 此题考查了勾股定理及勾股定理的逆定理,三角形的面积等知识,熟练掌握勾股定理及逆定理是解本题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
4.等式[(-6)-□]÷(-121)=0中,□表示的数是( )
| A. | 6 | B. | -6 | C. | 0 | D. | 115 |
5.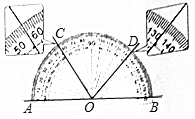 已知直线AB,射线OC,OD都在如图所示的量角器上,点O在直线AB上,则下列判断中不正确的是( )
已知直线AB,射线OC,OD都在如图所示的量角器上,点O在直线AB上,则下列判断中不正确的是( )
 已知直线AB,射线OC,OD都在如图所示的量角器上,点O在直线AB上,则下列判断中不正确的是( )
已知直线AB,射线OC,OD都在如图所示的量角器上,点O在直线AB上,则下列判断中不正确的是( )| A. | ∠AOC=56° | B. | ∠AOD=134° | C. | ∠AOC<∠COD | D. | ∠BOD与∠BOC互补 |
6.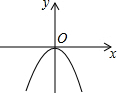 已知二次函数y=ax2的图象如图所示,则关于x的一元二次方程x2+x+a-1=0的根的存在情况是( )
已知二次函数y=ax2的图象如图所示,则关于x的一元二次方程x2+x+a-1=0的根的存在情况是( )
 已知二次函数y=ax2的图象如图所示,则关于x的一元二次方程x2+x+a-1=0的根的存在情况是( )
已知二次函数y=ax2的图象如图所示,则关于x的一元二次方程x2+x+a-1=0的根的存在情况是( )| A. | 没有实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 无法确定 |
 如图,已知∠EGB=90°,AD⊥BG,∠E=∠F.求证:AD是∠BAC平分线.
如图,已知∠EGB=90°,AD⊥BG,∠E=∠F.求证:AD是∠BAC平分线.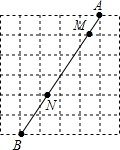 如图,在6×6的正方形网格中,连结两格点A,B,线段AB与网格线的交点为M、N,则AM:MN:NB为1:3:2.
如图,在6×6的正方形网格中,连结两格点A,B,线段AB与网格线的交点为M、N,则AM:MN:NB为1:3:2.