题目内容
6.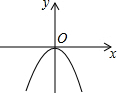 已知二次函数y=ax2的图象如图所示,则关于x的一元二次方程x2+x+a-1=0的根的存在情况是( )
已知二次函数y=ax2的图象如图所示,则关于x的一元二次方程x2+x+a-1=0的根的存在情况是( )| A. | 没有实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 无法确定 |
分析 先利用二次函数判断a<0,再计算判别式的值,然后根据判别式的意义判断方程根的情况.
解答 解:根据图象得a<0,
∵△=12-4(a-1)=5-4a,
而a<0,
∴△>0,
∴关于x的一元二次方程x2+x+a-1=0的有两个不相等的实数根.
故选C.
点评 本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
17.某班学生军训射击,有m人各打中a环,n人各打中b环,那么该班打中a环和b环学生的平均环数是( )
| A. | $\frac{a+b}{m+n}$ | B. | $\frac{1}{2}$($\frac{a}{m}$+$\frac{b}{n}$) | C. | $\frac{am+bn}{m+n}$ | D. | $\frac{1}{2}$(am+bn) |
18.计算-0.32÷0.5×2÷(-2)3的结果是( )
| A. | $\frac{9}{100}$ | B. | -$\frac{9}{100}$ | C. | $\frac{9}{200}$ | D. | -$\frac{9}{200}$ |
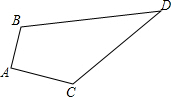 如图,四边形ABCD中,AB=3cm,AC=4cm,BD=13cm,CD=12cm,且∠A=90°,求△BCD的面积.
如图,四边形ABCD中,AB=3cm,AC=4cm,BD=13cm,CD=12cm,且∠A=90°,求△BCD的面积.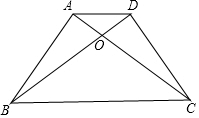 如图所示,AB⊥AC,DC⊥BD,AB=DC,求证:△ABD≌△DCA.
如图所示,AB⊥AC,DC⊥BD,AB=DC,求证:△ABD≌△DCA.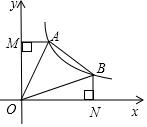 如图,直线y=-x+b(b>0)与双曲线y=$\frac{k}{x}$(x>0)交于A、B两点,连接OA、OB,AM⊥y轴于M,BN⊥x轴于N,现有以下结论:
如图,直线y=-x+b(b>0)与双曲线y=$\frac{k}{x}$(x>0)交于A、B两点,连接OA、OB,AM⊥y轴于M,BN⊥x轴于N,现有以下结论: