题目内容
8.对于任意的有理数a、b、c、d,我们规定$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc.如:$|\begin{array}{l}{(-2)}&{(-4)}\\{3}&{5}\end{array}|$=(-2)×5-(-4)×3=2,据这一规定,解答下列问题:(1)计算:$|\begin{array}{l}{(-2)}&{(-3)}\\{4}&{6}\end{array}|$的值;
(2)比较大小:$|\begin{array}{l}{2}&{3}\\{(-4)}&{(-5)}\end{array}|$<$|\begin{array}{l}{3}&{(-5)}\\{2}&{(-4)}\end{array}|$(填“>”或“=”或“<”).
(3)化简:$|\begin{array}{l}{(x+3y)}&{2x}\\{3y}&{(2x+y)}\end{array}|$.
分析 (1)原式利用题中的新定义计算即可得到结果;
(2)各式利用题中新定义计算,比较即可;
(3)原式利用题中新定义计算即可.
解答 解:(1)原式=-2×6-4×(-3)=-12+12=0;
(2)$|\begin{array}{l}{2}&{3}\\{(-4)}&{(-5)}\end{array}|$=-10+12=2,$|\begin{array}{l}{3}&{(-5)}\\{2}&{(-4)}\end{array}|$=12+10=22,
则:$|\begin{array}{l}{2}&{3}\\{(-4)}&{(-5)}\end{array}|$<$|\begin{array}{l}{3}&{(-5)}\\{2}&{(-4)}\end{array}|$;
故答案为:<;
(3)原式=(x+3y)(2x+y)-6xy=2x2+7xy+3y2-6xy=2x2+xy+3y2.
点评 此题考查了整式的混合运算,有理数的大小比较,以及有理数的混合运算,弄清题中的新定义是解本题的关键.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目
3. 对任意正整数n,按下列程序计算,应输出答案为( )
对任意正整数n,按下列程序计算,应输出答案为( )
 对任意正整数n,按下列程序计算,应输出答案为( )
对任意正整数n,按下列程序计算,应输出答案为( )| A. | n2-n+1 | B. | n2-1 | C. | 3-n | D. | 1 |
20.下列命题中是真命题的是( )
| A. | 所有的矩形都相似 | |
| B. | 所有的直角三角形都相似 | |
| C. | 有一个角是50°的所有等腰三角形都相似 | |
| D. | 有一个角是100°的所有等腰三角形都相似 |
17.某班学生军训射击,有m人各打中a环,n人各打中b环,那么该班打中a环和b环学生的平均环数是( )
| A. | $\frac{a+b}{m+n}$ | B. | $\frac{1}{2}$($\frac{a}{m}$+$\frac{b}{n}$) | C. | $\frac{am+bn}{m+n}$ | D. | $\frac{1}{2}$(am+bn) |
18.计算-0.32÷0.5×2÷(-2)3的结果是( )
| A. | $\frac{9}{100}$ | B. | -$\frac{9}{100}$ | C. | $\frac{9}{200}$ | D. | -$\frac{9}{200}$ |
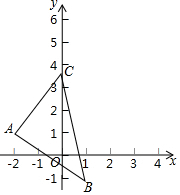 在平面直角坐标系中,A(-2,1),B(1,-1),C在y轴上,S△ABC=8,求点C的坐标.
在平面直角坐标系中,A(-2,1),B(1,-1),C在y轴上,S△ABC=8,求点C的坐标.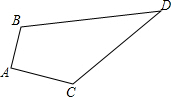 如图,四边形ABCD中,AB=3cm,AC=4cm,BD=13cm,CD=12cm,且∠A=90°,求△BCD的面积.
如图,四边形ABCD中,AB=3cm,AC=4cm,BD=13cm,CD=12cm,且∠A=90°,求△BCD的面积.