题目内容
12．计算：（1）$\sqrt{20}$+$\sqrt{125}$；
（2）（$\sqrt{48}$+$\sqrt{20}$）+（ $\sqrt{12}$-$\sqrt{5}$）．
分析 （1）首先化简二次根式，进而合并得出答案；
（2）首先化简二次根式，进而合并得出答案．
解答 解：（1）$\sqrt{20}$+$\sqrt{125}$
=2$\sqrt{5}$+5$\sqrt{5}$
=7$\sqrt{5}$；
（2）（$\sqrt{48}$+$\sqrt{20}$）+（ $\sqrt{12}$-$\sqrt{5}$）
=4$\sqrt{3}$+2$\sqrt{5}$+2$\sqrt{3}$-$\sqrt{5}$
=6$\sqrt{3}$+$\sqrt{5}$．
点评 此题主要考查了二次根式的加减运算，正确化简二次根式是解题关键．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
3．
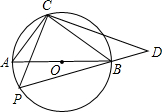如图，⊙O的直径为6，在⊙O上位于直径AB的异侧有定点C和动点P．已知BC：CA=4：3，P在半圆上运动，CP⊥CD交PB的延长线于D点．当点P运动到什么位置时，△PCD的面积最大为（ ）
如图，⊙O的直径为6，在⊙O上位于直径AB的异侧有定点C和动点P．已知BC：CA=4：3，P在半圆上运动，CP⊥CD交PB的延长线于D点．当点P运动到什么位置时，△PCD的面积最大为（ ）| A． | 36 | B． | 24 | C． | 18 | D． | 12 |
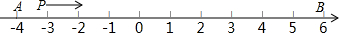如图，在数轴上点A表示的有理数为-4，点B表示的有理数为6，点P从点A出发以每秒2个单位长度的速度在数轴上沿由A到B方向运动，当点P到达点B后立即返回，仍然以每秒2个单位长度的速度运动至点A停止运动．设运动时间为t（单位：秒）．
4．在△ABC中，AD是∠BAC的平分线，若∠B=50°，∠C=70°，则∠CAD的度数是（ ）
| A． | 15° | B． | 30° | C． | 60° | D． | 120° |