题目内容
20.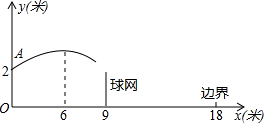 如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x-6)2+2.6,已知球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.
如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x-6)2+2.6,已知球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.(1)求y与x的函数关系式;
(2)球能否越过球网?
(3)球会不会出界?请说明理由.($\sqrt{39}≈6.2$)
分析 (1)把点A(0,2)代入关系式y=a(x-6)2+2.6,求出a的值,即可求出y与x的关系式;
(2)把x=9代入解析式求得y的值,若y>2.43,则球能越网,反之则不能;
(3)把x=18代入解析式求得y的值,若y>0则会出界,反之则不会.
解答 解:(1)把点A(0,2)代入关系式得:2=a(-6)2+2.6,
解得:a=-$\frac{1}{60}$,
则y与x的关系式为:y=-$\frac{1}{60}$(x-6)2+2.6;
(2)∵当x=9时,y=-$\frac{1}{60}$(9-6)2+2.6=2.45>2.43,
∴球能越过球网;
(3)∵当x=18时,y=-$\frac{1}{60}$(18-6)2+2.6=0.2>0,
∴球会出界.
点评 本题考查了二次函数的应用以及求范围的问题,可以利用临界点法求出自变量的值,再根据题意确定范围,难度一般.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
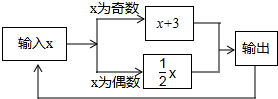 有一数值转换器,原理如图所示,若开始输入x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2015次输出的结果是4.
有一数值转换器,原理如图所示,若开始输入x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2015次输出的结果是4.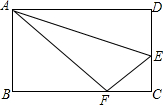 如图,把边长AD=10,AB=8的矩形沿AE对折,使点D落在BC上的点F处,求DE之长.
如图,把边长AD=10,AB=8的矩形沿AE对折,使点D落在BC上的点F处,求DE之长. 如图:作出与△ABC关x轴对称的图形△A1B1C1,并写出各点的坐标:
如图:作出与△ABC关x轴对称的图形△A1B1C1,并写出各点的坐标: