题目内容
已知正比例函数图象上的点到x轴的距离与到y轴距离的比为2:3,则函数的解析式为 .
考点:待定系数法求正比例函数解析式
专题:分类讨论
分析:设正比例函数解析式为y=kx,根据题意,正比例函数图象上的点的坐标可设为(3a,2a)或(3a,-2a),然后把它们分别代入y=kx可计算出对应的k的值,从而可确定正比例函数解析式.
解答:解:设正比例函数解析式为y=kx,
∵正比例函数图象上的点到x轴的距离与到y轴距离的比为2:3,
∴正比例函数图象上的点的坐标可设为(3a,2a)或(3a,-2a),
∴k•3a=2a或k•3a=-2a
∴k=
或-
,
∴正比例函数解析式为y=
x或y=-
x.
故答案为y=
x或y=-
x.
∵正比例函数图象上的点到x轴的距离与到y轴距离的比为2:3,
∴正比例函数图象上的点的坐标可设为(3a,2a)或(3a,-2a),
∴k•3a=2a或k•3a=-2a
∴k=
| 2 |
| 3 |
| 2 |
| 3 |
∴正比例函数解析式为y=
| 2 |
| 3 |
| 2 |
| 3 |
故答案为y=
| 2 |
| 3 |
| 2 |
| 3 |
点评:本题考查了待定系数法求正比例函数的解析式:设正比例函数解析式为y=kx,然后把一组对应值代入求出k,从而得到正比例函数解析式.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 如图,点E,F分别是矩形ABCD的边AD,BC的三等分点(距D、C近),若矩形ABFE与矩形ABCD相似,则矩形ABCD的AD:AB是
如图,点E,F分别是矩形ABCD的边AD,BC的三等分点(距D、C近),若矩形ABFE与矩形ABCD相似,则矩形ABCD的AD:AB是 已知:如图,在?ABCD中,AC、BD相交于点O,点E、F分别在OB、OD上,且OE=OF.求证:四边形AECF是平行四边形.
已知:如图,在?ABCD中,AC、BD相交于点O,点E、F分别在OB、OD上,且OE=OF.求证:四边形AECF是平行四边形. 如图,锐角三角形ABC内接于⊙O,D、E分别为OA与BC的中点,连接DE.已知∠ABC=3∠ODE,∠ACB=5∠ODE,求∠OCE的度数.
如图,锐角三角形ABC内接于⊙O,D、E分别为OA与BC的中点,连接DE.已知∠ABC=3∠ODE,∠ACB=5∠ODE,求∠OCE的度数. 如图,E是平行四边形ABCD的AB边的中点,且AD=10cm,那么OE=
如图,E是平行四边形ABCD的AB边的中点,且AD=10cm,那么OE=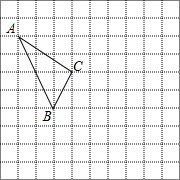 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,B的坐标分别为(-4,3),(2,-1).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,B的坐标分别为(-4,3),(2,-1).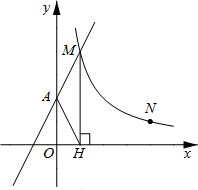 如图,直线y1=2x+2与y轴交于A点,与反比例函数y2=
如图,直线y1=2x+2与y轴交于A点,与反比例函数y2=