题目内容
 如图,锐角三角形ABC内接于⊙O,D、E分别为OA与BC的中点,连接DE.已知∠ABC=3∠ODE,∠ACB=5∠ODE,求∠OCE的度数.
如图,锐角三角形ABC内接于⊙O,D、E分别为OA与BC的中点,连接DE.已知∠ABC=3∠ODE,∠ACB=5∠ODE,求∠OCE的度数.考点:圆周角定理
专题:
分析:首先设∠ODE=x°,则∠ABC=3∠ODE=3x°,∠ACB=5∠ODE=5x°,利用三角形内角和定理,可求得∠BAC,又由E是BC的中点,求得∠EOC=∠BAC,由圆周角定理可求得∠AOC,继而可得∠ODE=∠OED,则可得OE=OD=
OA=
OC,继而求得答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:设∠ODE=x°,
则∠ABC=3∠ODE=3x°,∠ACB=5∠ODE=5x°,
∴∠BAC=180°-∠ABC-∠ACB=180°-8x°,
∵E是BC的中点,
∴∠COE=
∠BOC,OE⊥BC,
∵∠BOC=2∠BAC,
∴∠COE=∠BAC=180°-8x°,
∵∠AOC=2∠ABC=6x°,
∴∠AOE=∠AOC+∠COE=180°-2x°,
∴∠ODE=180°-∠OED-∠AOE=180°-x°-(180°-2x°)=x°,
∴∠ODE=∠OED,
∴OE=OD=
OA=
OC,
∴∠OCE=30°.
则∠ABC=3∠ODE=3x°,∠ACB=5∠ODE=5x°,
∴∠BAC=180°-∠ABC-∠ACB=180°-8x°,
∵E是BC的中点,
∴∠COE=
| 1 |
| 2 |
∵∠BOC=2∠BAC,
∴∠COE=∠BAC=180°-8x°,
∵∠AOC=2∠ABC=6x°,
∴∠AOE=∠AOC+∠COE=180°-2x°,
∴∠ODE=180°-∠OED-∠AOE=180°-x°-(180°-2x°)=x°,
∴∠ODE=∠OED,
∴OE=OD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OCE=30°.
点评:此题考查了圆周角定理以及等腰三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 如图,直线y=-
如图,直线y=- 已知反比例函数y=
已知反比例函数y=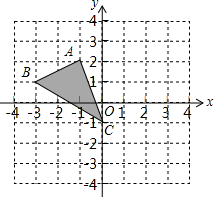 如图,已知△ABC的三个顶点恰好是网格的格点,按照图中的位置建立平面直角坐标系:
如图,已知△ABC的三个顶点恰好是网格的格点,按照图中的位置建立平面直角坐标系: