题目内容
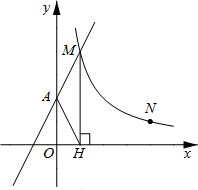 如图,直线y1=2x+2与y轴交于A点,与反比例函数y2=
如图,直线y1=2x+2与y轴交于A点,与反比例函数y2=| k |
| x |
(1)求点M的坐标与k的值;
(2)直接写出使y2>y1成立的自变量取值范围;
(3)点N(a,1)是反比例函数y2=
| k |
| x |
考点:反比例函数综合题
专题:
分析:(1)根据直线解析式求A点坐标,得OA的长度;根据三角函数定义可求OH的长度,得点M的横坐标;根据点M在直线上可求点M的坐标,从而可求K的值;
(2)根据(1)中求得的k值,得出反比例函数的解析式,然后求出y2>y1成立的自变量取值范围;
(3)根据反比例函数解析式可求N点坐标;作点N关于x轴的对称点N1,连接MN1与x轴的交点就是满足条件的P点位置.
(2)根据(1)中求得的k值,得出反比例函数的解析式,然后求出y2>y1成立的自变量取值范围;
(3)根据反比例函数解析式可求N点坐标;作点N关于x轴的对称点N1,连接MN1与x轴的交点就是满足条件的P点位置.
解答:解:(1)由y1=2x+2可知A(0,2),即OA=2,
∵tan∠AHO=2,
∴OH=1,
∵MH⊥x轴,
∴点M的横坐标为1.
∵点M在直线y=2x+2上,
∴点M的纵坐标为4,
即M(1,4),
∵点M在y2=
上,
∴k=1×4=4;
(2)由(1)得:y2=
,
当y2>y1时,
>2x+2,
解得:-2<x<1,
∵x>0,
∴自变量的取值范围为:0<x<1;
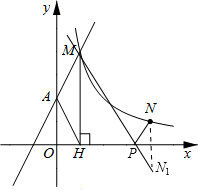
(3)存在.
过点N作N关于x轴的对称点N1,连接MN1,交x轴于P(如图所示).此时PM+PN最小.
∵点N(a,1)在反比例函数y2=
(x>0)上,
∴a=4.即点N的坐标为(4,1),
∵N与N1关于x轴的对称,N点坐标为(4,1),
∴N1的坐标为(4,-1),
设直线MN1的解析式为y=kx+b.
由
,
解得:k=-
,b=
.
∴直线MN1的解析式为y=-
x+
.
令y=0,得x=
.
∴P点坐标为(
,0).
∵tan∠AHO=2,
∴OH=1,
∵MH⊥x轴,
∴点M的横坐标为1.
∵点M在直线y=2x+2上,
∴点M的纵坐标为4,
即M(1,4),
∵点M在y2=
| k |
| x |
∴k=1×4=4;

(2)由(1)得:y2=
| 4 |
| x |
当y2>y1时,
| 4 |
| x |
解得:-2<x<1,
∵x>0,
∴自变量的取值范围为:0<x<1;
(3)存在.
过点N作N关于x轴的对称点N1,连接MN1,交x轴于P(如图所示).此时PM+PN最小.
∵点N(a,1)在反比例函数y2=
| x |
| 4 |
∴a=4.即点N的坐标为(4,1),
∵N与N1关于x轴的对称,N点坐标为(4,1),
∴N1的坐标为(4,-1),
设直线MN1的解析式为y=kx+b.
由
|
解得:k=-
| 5 |
| 3 |
| 17 |
| 3 |
∴直线MN1的解析式为y=-
| 5 |
| 3 |
| 17 |
| 3 |
令y=0,得x=
| 17 |
| 5 |
∴P点坐标为(
| 17 |
| 5 |
点评:此题考查了一次函数和反比例函数的综合应用,涉及的知识有:待定系数法确定函数解析式,一次函数与反比例函数的交点问题,以及线路最短问题,得出P点位置是解题关键.

练习册系列答案
相关题目
一辆汽车匀速行驶,若在a秒内行驶
米,则它在2分钟内可行驶( )
| m |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列各组中的两项,属于同类项的有( )
①2x2y与-
x2y;②3a2bc与a2cb;③x3与x;④1与
;⑤m2n与mn2.
①2x2y与-
| 1 |
| 2 |
| 1 |
| 8 |
| A、2组 | B、3组 | C、4组 | D、5组 |
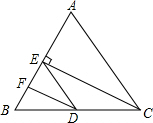 如图所示,在△ABC中,CE⊥AB于点E,点D在BC上,∠BED=∠A,CE平分∠ACB,DF平分∠BDE,求证:DF⊥AB.
如图所示,在△ABC中,CE⊥AB于点E,点D在BC上,∠BED=∠A,CE平分∠ACB,DF平分∠BDE,求证:DF⊥AB.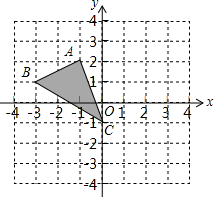 如图,已知△ABC的三个顶点恰好是网格的格点,按照图中的位置建立平面直角坐标系:
如图,已知△ABC的三个顶点恰好是网格的格点,按照图中的位置建立平面直角坐标系: 如图,已知四边形ABED∽四边形BCGF∽四边形CAIH,记四边形ABED、四边形BFGC和四边形CAIH的面积分别为S3、S2、S1,若S1+S2=S3,求证:△ABC为直角三角形.
如图,已知四边形ABED∽四边形BCGF∽四边形CAIH,记四边形ABED、四边形BFGC和四边形CAIH的面积分别为S3、S2、S1,若S1+S2=S3,求证:△ABC为直角三角形. 如图,在平面直角坐标系中,直线AB与x轴、y轴分别相交于点A(6,0)、B(0,8).点C(0,m)是线段OB上动点,过点C作CE⊥AB于点E,点D为
如图,在平面直角坐标系中,直线AB与x轴、y轴分别相交于点A(6,0)、B(0,8).点C(0,m)是线段OB上动点,过点C作CE⊥AB于点E,点D为